文章参考：https://labuladong.github.io/algo/

nSum问题

文章参考

参考链接：一个方法团灭 NSUM 问题

参考链接：一个函数秒杀 2Sum 3Sum 4Sum 问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 1：两数之和
• 15：三数之和
• 18：四数之和
• 167：两数之和 II - 输入有序数组
• 剑指 Offer II 007： 数组中和为 0 的三个数

/* 注意：调用这个函数之前一定要先给 nums 排序 */

// nums:排序后的数组，n：nSum的n，start：nums中开始计算的起始索引，target：数组需要满足的target
const nSumTarget = (nums: number[], n:number, start:number, target:number):number[][] => {
    let size = nums.length;
    let result = [];
    
    // 排除掉比2Sum还少或者数组元素个数比n还小的情况
    if(n <2 || size < n) return result;

    if(n === 2){//2Sum
        let low = start;//左指针
        let high = size -1;//右指针
        while(low < high){//左右指针还没相遇，还没处理完
            let sum = nums[low] + nums[high];
            let leftValue = nums[low];
            let rightValue = nums[high];

            if(sum < target){//左右指针对应两数相加比target小
                //左指针往右，同时要跳过重复元素
                while(low < high && leftValue === nums[low]){
                    low ++;
                }
            }else if(sum > target){//左右指针对应两数相加比target大
                //左指针往左，同时要跳过重复元素
                while(low < high && rightValue === nums[high]){
                    high --;
                }
            }else {//想等
                result.push([leftValue,rightValue]);
                // 左右分别移动指针，去除重复元素
                while(low < high && leftValue === nums[low]){
                    low ++;
                }
                while(low < high && rightValue === nums[high]){
                    high --;
                }
            }
        }
    }else {// nSum问题，递归处理
        for(let i = start;i< size; i++){
            let subRes = nSumTarget(nums,n-1,i+1,target-nums[i]);//当前n-1的sum结果
            for(let arr of subRes){
                arr.push(nums[i]);//把当前的放进结果中
                result.push(arr);
            }
            while(i < size - 1 && nums[i] === nums[i+1]){//去掉重复元素
                i++;
            }

        }
    }
    return result;
}

因此，如果处理3Sum问题，就是nSumTarget(nums,3,0,0);

滑动窗口问题

文章参考

参考链接：我写了首诗，把滑动窗口算法算法变成了默写题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 3：无重复字符的最长子串
• 76：最小覆盖子串
• 438：找到字符串中所有字母异位词
• 567：字符串的排列
• 剑指 Offer 48：最长不含重复字符的子字符串
• 剑指 Offer II 014：字符串中的变位词
• 剑指 Offer II 015：字符串中的所有变位词
• 剑指 Offer II 016：不含重复字符的最长子字符串
• 剑指 Offer II 017：含有所有字符的最短字符串

/* 滑动窗口算法框架 */

function slidingWindow(s: string) {
    let left = 0;
    let right = 0;

    let window = new Map();

    // let need = new Map()//如果有必要构建target的map

    // let result = ...

    while(right < s.length){//右指针还没到最后
        let r = s[right];//右指针对应字符
        right++;//增大窗口

        // 进行窗口内数据的一系列更新
        // ...
        // window.set

        // 判断左侧窗口是否要收缩
        while(window needs shrink){
            let l = s[left];//左指针对应字符
            left ++;//窗口收缩

            // 进行窗口内数据的一系列更新
            // ...
            // window.set
        }

        // 计算result的值
        // result = ...
    }

    // return result;
}

双指针解决数组问题

文章参考

参考链接：双指针技巧秒杀七道数组题目

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 5：最长回文子串
• 26：删除有序数组中的重复项
• 27：移除元素
• 83：删除排序链表中的重复元素
• 167：两数之和 II - 输入有序数组
• 283：移动零
• 344：反转字符串
• 剑指 Offer 57：和为s的两个数字
• 剑指 Offer II 006：排序数组中两个数字之和

双指针技巧主要分为两类：左右指针 和 快慢指针 。

对于单链表来说，大部分技巧都属于快慢指针。在数组中并没有真正意义上的指针，但我们可以把索引当做数组中的指针，这样也可以在数组中施展双指针技巧，本文主要讲数组相关的双指针算法。

一、快慢指针技巧

数组问题中比较常见的快慢指针技巧，是让你原地修改数组。如第 26 题「 删除有序数组中的重复项」，让你在有序数组去重：

高效解决这道题就要用到快慢指针技巧：

我们让慢指针 slow 走在后面，快指针 fast 走在前面探路，找到一个不重复的元素就赋值给 slow 并让 slow 前进一步。

这样，就保证了 nums[0..slow] 都是无重复的元素，当 fast 指针遍历完整个数组 nums 后，nums[0..slow] 就是整个数组去重之后的结果。

除了让你在有序数组/链表中去重，题目还可能让你对数组中的某些元素进行「原地删除」。比如力扣第 27 题「 移除元素」：

如果 fast 遇到值为 val 的元素，则直接跳过，否则就赋值给 slow 指针，并让 slow 前进一步。

接下来看看力扣第 283 题「 移动零」：

题目让我们将所有 0 移到最后，其实就相当于移除 nums 中的所有 0，然后再把后面的元素都赋值为 0 即可。

数组中另一大类快慢指针的题目就是「滑动窗口算法」。上面也提到了。left 指针在后，right 指针在前，两个指针中间的部分就是「窗口」，算法通过扩大和缩小「窗口」来解决某些问题。

二、左右指针的常用算法

1、二分查找

int binarySearch(int[] nums, int target) {
    // 一左一右两个指针相向而行
    int left = 0, right = nums.length - 1;
    while(left <= right) {
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; 
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

2、两数之和

看下力扣第 167 题「 两数之和 II」：

只要数组有序，就应该想到双指针技巧。这道题的解法有点类似二分查找，通过调节 left 和 right 就可以调整 sum 的大小.

3、反转数组

一般编程语言都会提供 reverse 函数，其实这个函数的原理非常简单，力扣第 344 题「 反转字符串」就是类似的需求，让你反转一个 char[] 类型的字符数组

void reverseString(char[] s) {
    // 一左一右两个指针相向而行
    int left = 0, right = s.length - 1;
    while (left < right) {
        // 交换 s[left] 和 s[right]
        char temp = s[left];
        s[left] = s[right];
        s[right] = temp;
        left++;
        right--;
    }
}

4、回文串判断

给你一个字符串，让你用双指针技巧从中找出最长的回文串，你会做吗？

这就是力扣第 5 题「 最长回文子串」：

找回文串的难点在于，回文串的的长度可能是奇数也可能是偶数，解决该问题的核心是从中心向两端扩散的双指针技巧。

如果回文串的长度为奇数，则它有一个中心字符；如果回文串的长度为偶数，则可以认为它有两个中心字符.所以我们可以先实现这样一个函数：

// 在 s 中寻找以 s[l] 和 s[r] 为中心的最长回文串
String palindrome(String s, int l, int r) {
    // 防止索引越界
    while (l >= 0 && r < s.length()
            && s.charAt(l) == s.charAt(r)) {
        // 双指针，向两边展开
        l--; r++;
    }
    // 返回以 s[l] 和 s[r] 为中心的最长回文串
    return s.substring(l + 1, r);
}

那么回到最长回文串的问题，解法的大致思路就是：

for 0 <= i < len(s):
    找到以 s[i] 为中心的回文串
    找到以 s[i] 和 s[i+1] 为中心的回文串
    更新答案

翻译成代码，就可以解决最长回文子串这个问题：

String longestPalindrome(String s) {
    String res = "";
    for (int i = 0; i < s.length(); i++) {
        // 以 s[i] 为中心的最长回文子串
        String s1 = palindrome(s, i, i);
        // 以 s[i] 和 s[i+1] 为中心的最长回文子串
        String s2 = palindrome(s, i, i + 1);
        // res = longest(res, s1, s2)
        res = res.length() > s1.length() ? res : s1;
        res = res.length() > s2.length() ? res : s2;
    }
    return res;
}

你应该能发现最长回文子串使用的左右指针和之前题目的左右指针有一些不同：之前的左右指针都是从两端向中间相向而行，而回文子串问题则是让左右指针从中心向两端扩展。不过这种情况也就回文串这类问题会遇到，所以我也把它归为左右指针了。

接雨水问题

文章参考

参考链接：如何高效解决接雨水问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 11：盛最多水的容器
• 42：接雨水

力扣第 42 题「 接雨水」挺有意思，在面试题中出现频率还挺高的。对于这种问题，我们不要想整体，而应该去想局部；就像之前的文章写的动态规划问题处理字符串问题，不要考虑如何处理整个字符串，而是去思考应该如何处理每一个字符。

双指针解法:这种解法的思路是完全相同的，但在实现手法上非常巧妙，我们这次也不要用备忘录提前计算了，而是用双指针边走边算，节省下空间复杂度。

重点一定要考虑局部，而不是整体，一个个柱子去考虑，而不是想整体。

下面我们看一道和接雨水问题非常类似的题目，力扣第 11 题「 盛最多水的容器」：

接雨水问题给出的类似一幅直方图，每个横坐标都有宽度，而本题给出的每个横坐标是一条竖线，没有宽度。

解决这道题的思路依然是双指针技巧：

用 left 和 right 两个指针从两端向中心收缩，一边收缩一边计算 [left, right] 之间的矩形面积，取最大的面积值即是答案。

回溯算法套路

文章参考

参考链接：回溯算法解题套路框架

参考链接：回溯算法秒杀所有排列-组合-子集问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 17：电话号码的字母组合
• 39：组合总和
• 40：组合总和 II
• 46：全排列
• 47：全排列 II
• 51：N皇后
• 52：N皇后 II
• 77：组合
• 78：子集
• 90：子集 II
• 216：组合总和 III
• 剑指 Offer II 079：所有子集
• 剑指 Offer II 080：含有 k 个元素的组合
• 剑指 Offer II 081：允许重复选择元素的组合
• 剑指 Offer II 082：含有重复元素集合的组合
• 剑指 Offer II 083：没有重复元素集合的全排列
• 剑指 Offer II 084：含有重复元素集合的全排列

其实回溯算法和我们常说的 DFS 算法非常类似，本质上就是一种暴力穷举算法。回溯算法和 DFS 算法的细微差别是：回溯算法是在遍历「树枝」，DFS 算法是在遍历「节点」，

废话不多说，直接上回溯算法框架，解决一个回溯问题，实际上就是一个决策树的遍历过程，站在回溯树的一个节点上，你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

如果你不理解这三个词语的解释，没关系，我们后面会用「全排列」和「N 皇后问题」这两个经典的回溯算法问题来帮你理解这些词语是什么意思，现在你先留着印象。

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
        
for 选择 in 选择列表:
    做选择
    backtrack(路径, 选择列表)
    撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列。

/*
 * @lc app=leetcode.cn id=17 lang=typescript
 *
 * [17] 电话号码的字母组合
 */

// @lc code=start
function letterCombinations(digits: string): string[] {
    if (!digits) {
        return []
    }

    const map = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"];
    let res: string[] = [];

    // digits 和start 构成选择列表，tarck为路径
    const backtrack = (digits: string, start: number, track: string[]) => {
        // if 满足结束条件:
        if (track.length === digits.length) {
            // result.add(路径)
            res.push(Array.from(track).join(""));
            return;
        }

        for (let i = start; i < digits.length; i++) {
            const digit = digits[i];
            // for 选择 in 选择列表:
            for (const ch of map[parseInt(digit)]) {

                // 做选择
                track.push(ch);

                //  backtrack(路径, 选择列表)
                backtrack(digits, i + 1, track);

                // 撤销选择
                track.pop();
            }

        }
    }

    backtrack(digits, 0, []);

    return res;
};
// @lc code=end

无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：

形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。

以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。

形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。

以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。

形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。

以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。

但无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可把这些问题一网打尽。

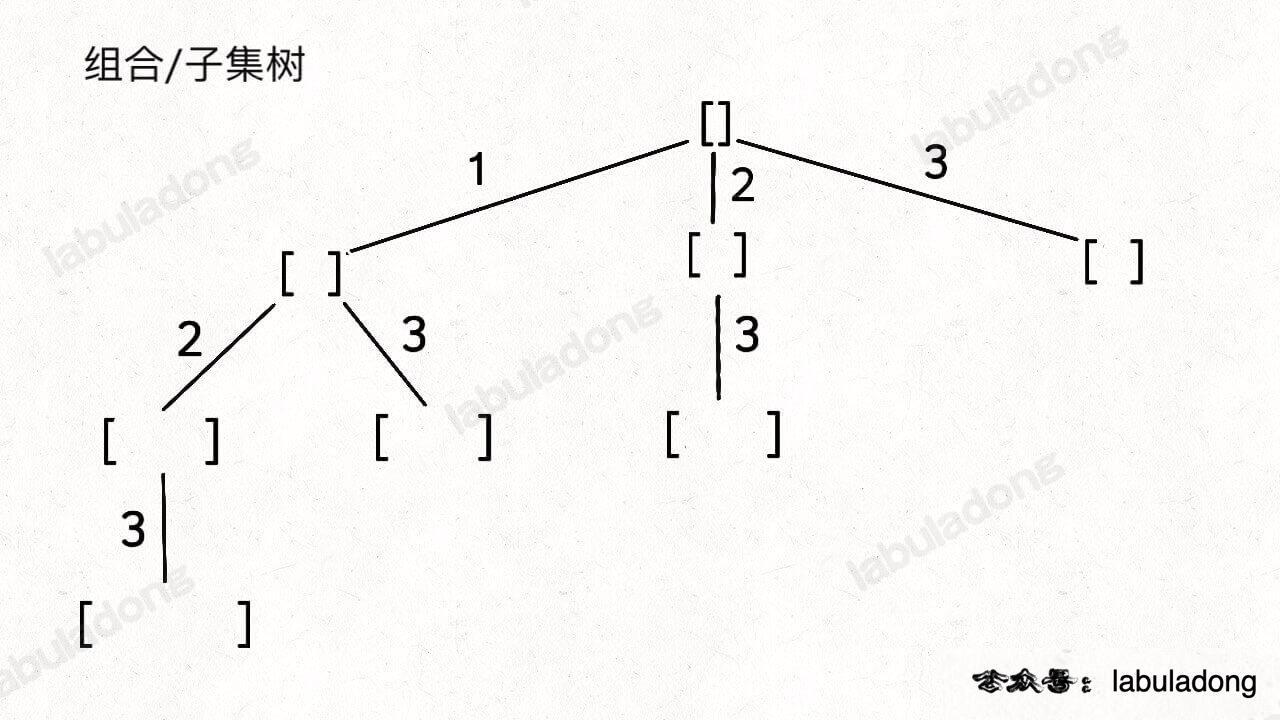
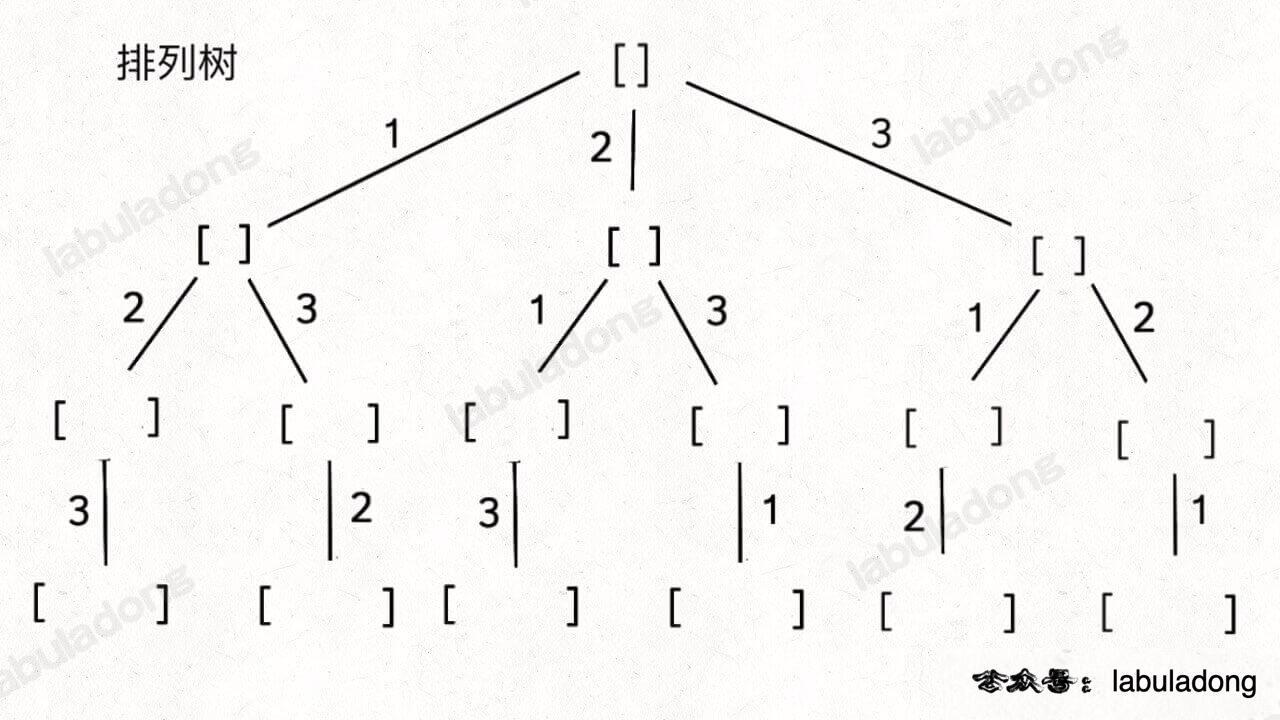
具体来说，你需要先阅读并理解前文 回溯算法核心套路，然后记住如下子集问题和排列问题的回溯树，就可以解决所有排列组合子集相关的问题：

为什么只要记住这两种树形结构就能解决所有相关问题呢？

首先，组合问题和子集问题其实是等价的，这个后面会讲；至于之前说的三种变化形式，无非是在这两棵树上剪掉或者增加一些树枝罢了。

子集（元素无重不可复选）

/*
 * @lc app=leetcode.cn id=78 lang=typescript
 *
 * [78] 子集
 */

// @lc code=start
function subsets(nums: number[]): number[][] {
    // 元素无重不可复选

    let res: number[][] = [];

    const backtrack = (nums: number[], start: number, track: number[]) => {
        // 每个节点都是一个子集
        res.push(Array.from(track));

        for (let i = start; i < nums.length; i++) {
            track.push(nums[i]);

            // start控制数值的生长避免产生重复的子集
            backtrack(nums, i + 1, track);

            track.pop();
        }
    }

    backtrack(nums, 0, []);

    return res;
};
// @lc code=end

组合（元素无重不可复选）

/*
 * @lc app=leetcode.cn id=77 lang=typescript
 *
 * [77] 组合
 */

// @lc code=start
function combine(n: number, k: number): number[][] {
    let res: number[][] = [];

    const backtrack = (n: number, start: number, track: number[]) => {
        if (track.length === k) {
            res.push(Array.from(track));
            return;
        }

        for (let i = start; i < n; i++) {
            track.push(i + 1);

            backtrack(n, i + 1, track);

            track.pop();
        }
    }

    backtrack(n, 0, []);

    return res;

};
// @lc code=end

排列（元素无重不可复选）

/*
 * @lc app=leetcode.cn id=46 lang=typescript
 *
 * [46] 全排列
 */

// @lc code=start
function permute(nums: number[]): number[][] {
    let res: number[][] = [];

    const backtrack = (nums: number[], track: number[], used: boolean[]) => {
        if (track.length === nums.length) {
            res.push(Array.from(track));
            return;
        }

        // 因为是全排列，所以以前用过的不能使用了，需要used来标记一下是否使用过
        // 注意used是一条垂直线上使用的，不是横着使用的
        for (let i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }

            track.push(nums[i]);
            used[i] = true;

            backtrack(nums, track, used);

            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums, [], []);

    return res;
};
// @lc code=end

子集/组合（元素可重不可复选）

/*
 * @lc app=leetcode.cn id=90 lang=typescript
 *
 * [90] 子集 II
 */

// @lc code=start
function subsetsWithDup(nums: number[]): number[][] {
    let res: number[][] = [];

    nums.sort((a, b) => a - b);

    const backtrack = (nums: number[], start: number, track: number[]) => {
        res.push(Array.from(track));

        for (let i = start; i < nums.length; i++) {

            if (i > start && nums[i] === nums[i - 1]) {
                continue;
            }

            track.push(nums[i]);

            backtrack(nums, i + 1, track);

            track.pop();

        }
    }

    backtrack(nums, 0, []);

    return res;
};
// @lc code=end

/*
 * @lc app=leetcode.cn id=40 lang=typescript
 *
 * [40] 组合总和 II
 */

// @lc code=start
function combinationSum2(candidates: number[], target: number): number[][] {
    let res: number[][] = [];

    // 只要元素重复，就要排序
    candidates.sort((a: number, b: number) => a - b)

    const backtrack = (candidates: number[], start: number, track: number[], sum: number) => {
        if (sum === target) {
            res.push(Array.from(track));
            return;
        } else if (sum > target) {
            return;
        }

        for (let i = start; i < candidates.length; i++) {
            // 如果有2个1样的，就没必要重复算了
            if (i > start && candidates[i] === candidates[i - 1]) {
                continue;
            }

            track.push(candidates[i]);
            sum += candidates[i];

            backtrack(candidates, i + 1, track, sum);

            track.pop();
            sum -= candidates[i];

        }
    }

    backtrack(candidates, 0, [], 0)

    return res;
};
// @lc code=end

排列（元素可重不可复选）

/*
 * @lc app=leetcode.cn id=47 lang=typescript
 *
 * [47] 全排列 II
 */

// @lc code=start
function permuteUnique(nums: number[]): number[][] {
    let res: number[][] = [];
    nums.sort((a, b) => a - b);

    const backtrack = (nums: number[], track: number[], used: boolean[]) => {
        if (track.length === nums.length) {
            res.push(Array.from(track));
            return;
        }

        let preval = -999;//随便一个特殊值

        for (let i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }

            if (nums[i] === preval) {
                continue;
            }

            track.push(nums[i]);
            used[i] = true;

            preval = nums[i];

            backtrack(nums, track, used);

            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums, [], []);

    return res;
};
// @lc code=end

子集/组合（元素无重可复选）

/*
 * @lc app=leetcode.cn id=39 lang=typescript
 *
 * [39] 组合总和
 */

// @lc code=start
function combinationSum(candidates: number[], target: number): number[][] {
    let res: number[][] = [];

    const backtrack = (candidates: number[], start: number, track: number[], sum: number) => {
        if (sum === target) {
            res.push(Array.from(track));
            return;
        } else if (sum > target) {
            return;
        }

        // candidates = [2,3,6,7], target = 7
        // 这里是start还是从0开始，取决于
        // 第一次选择：当选择完2后，第二次可以选择2,3,6,7
        // 第二次选择：当选择完3后，第二次可选择3,6,7，而不是2,3,6，7，因为前面选择过了2-3-...，无需重复，因为不是全排列
        for (let i = start; i < candidates.length; i++) {
            track.push(candidates[i]);
            sum += candidates[i];

            backtrack(candidates, i, track, sum);

            sum -= candidates[i];
            track.pop();

        }
    }

    backtrack(candidates, 0, [], 0);

    return res;
};
// @lc code=end

排列（元素无重可复选）

List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();

public List<List<Integer>> permuteRepeat(int[] nums) {
    backtrack(nums);
    return res;
}

// 回溯算法核心函数
void backtrack(int[] nums) {
    // base case，到达叶子节点
    if (track.size() == nums.length) {
        // 收集叶子节点上的值
        res.add(new LinkedList(track));
        return;
    }

    // 回溯算法标准框架
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        track.add(nums[i]);
        // 进入下一层回溯树
        backtrack(nums);
        // 取消选择
        track.removeLast();
    }
}

最后总结

形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，backtrack 核心代码如下：

/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}

/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

//先排序
Arrays.sort(nums);

/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 剪枝逻辑，跳过值相同的相邻树枝
        if (i > start && nums[i] == nums[i - 1]) {
            continue;
        }
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}


Arrays.sort(nums);
/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

/* 组合/子集问题回溯算法框架 */
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i);
        // 撤销选择
        track.removeLast();
    }
}


/* 排列问题回溯算法框架 */
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.removeLast();
    }
}

双指针解决链表问题

文章参考

参考链接：双指针技巧秒杀七道链表题目

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 19：删除链表的倒数第 N 个结点
• 21：合并两个有序链表
• 23：合并K个升序链表
• 86：分隔链表
• 141：环形链表
• 142：环形链表 II
• 160：相交链表
• 876：链表的中间结点
• 剑指 Offer 22：链表中倒数第k个节点
• 剑指 Offer 25：合并两个排序的链表
• 剑指 Offer 52：两个链表的第一个公共节点
• 剑指 Offer II 021：删除链表的倒数第 n 个结点
• 剑指 Offer II 022：链表中环的入口节点
• 剑指 Offer II 023：两个链表的第一个重合节点
• 剑指 Offer II 078：合并排序链表

本文就总结一下单链表的基本技巧，每个技巧都对应着至少一道算法题：

1、合并两个有序链表

2、链表的分解

3、合并 k 个有序链表

4、寻找单链表的倒数第 k 个节点

5、寻找单链表的中点

6、判断单链表是否包含环并找出环起点

7、判断两个单链表是否相交并找出交点

这些解法都用到了双指针技巧，所以说对于单链表相关的题目，双指针的运用是非常广泛的.

什么时候需要用虚拟头结点？

当你需要创造一条新链表的时候，可以使用虚拟头结点简化边界情况的处理。

手写实现Heap结构

文章参考

参考链接：二叉堆详解实现优先级队列

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Heap {
    data: ListNode[];
    comparator: Function;

    constructor(comparator = (a: ListNode, b: ListNode) => a.val < b.val, data = []) {
        this.comparator = comparator;
        this.data = data;
        this.heapify();
    }

    // 堆化
    heapify() {
        // 1个或者0个，没必要堆化了
        if (this.size() < 2) return;

        // 这为啥从中间开始？值堆化一半就够了？
        for (let i = Math.floor(this.size() / 2) - 1; i >= 0; i--) {
            this.bubbleDown(i);

        }
    }

    // 元素往上走
    bubbleUp(index: number) {
        while (index > 0) {
            const pIndex = (index - 1) >> 1; //注意：父节点位置，很有意思的一步

            // 往上走，所以要比较他和他爹谁大
            if (this.comparator(this.data[index], this.data[pIndex])) {
                this.swap(index, pIndex);//跟他爹换换位置
                index = pIndex;
            } else {
                break;
            }
        }
    }

    // 元素往下沉
    bubbleDown(index: number) {
        const lastIndex = this.size() - 1;

        while (true) {
            const leftIndex = index * 2 + 1;//左子节点index
            const rightIndex = index * 2 + 2;// 右子节点index
            let findIndex = index; //当前bubbleDown节点的位置

            // 左节点跟根节点对比，选择符合条件的
            if (leftIndex <= lastIndex && this.comparator(this.data[leftIndex], this.data[findIndex])) {
                findIndex = leftIndex;
            }

            // 右节点跟根节点对比，选择符合条件的上去
            if (rightIndex <= lastIndex && this.comparator(this.data[rightIndex], this.data[findIndex])) {
                findIndex = rightIndex;
            }

            // 说明有变化，做了交换
            if (index !== findIndex) {
                this.swap(index, findIndex);
                index = findIndex;
            } else {
                break;
            }
        }
    }

    // 交换两个元素位置
    swap(i: number, j: number) {
        [this.data[i], this.data[j]] = [this.data[j], this.data[i]];
    }

    // 返回堆顶元素
    peek() {
        return this.size() >= 0 ? this.data[0] : null;
    }

    // 往堆里面添加一个值
    offer(value: ListNode) {
        this.data.push(value);//添加一个元素，相当于放到了最右下角的子节点,index为数组最后一个
        this.bubbleUp(this.size() - 1);
    }

    // 移除堆顶元素，重新构建堆，返回删除的元素
    poll() {
        if (this.size() === 0) {
            return null;
        }
        // 把第一个扔到最后面去，然后把最后一个扔到第一个，然后让第1个往下沉。
        this.swap(0, this.size() - 1);
        let result = this.data.pop()!;
        this.bubbleDown(0);
        return result;
    }

    // 堆的大小
    size() {
        return this.data.length;
    }
}

括号问题

文章参考

参考链接：如何解决括号相关的问题

参考链接：回溯算法最佳实践：括号生成

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 20：有效的括号

• 921：使括号有效的最少添加

• 1541：平衡括号字符串的最少插入次数

• 22：括号生成

• 剑指 Offer II 085：生成匹配的括号

有关括号问题，你只要记住以下性质，思路就很容易想出来：

1、一个「合法」括号组合的左括号数量一定等于右括号数量，这个很好理解。

2、对于一个「合法」的括号字符串组合 p，必然对于任何 0 <= i < len(p) 都有：子串 p[0..i] 中左括号的数量都大于或等于右括号的数量。

二分搜索问题

文章参考

参考链接：我写了首诗，让你闭着眼睛也能写对二分搜索

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 34：在排序数组中查找元素的第一个和最后一个位置
• 704：二分查找
• 剑指 Offer 53 - I: 在排序数组中查找数字 I

二分查找并不简单，Knuth 大佬（发明 KMP 算法的那位）都说二分查找：思路很简单，细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿，但是二分查找真正的坑根本就不是那个细节问题，而是在于到底要给 mid 加一还是减一，while 里到底用 <= 还是 <。

二分查找框架

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。

另外提前说明一下，计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防止了 left 和 right 太大，直接相加导致溢出的情况。

寻找一个数（基本的二分搜索）

int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

寻找左侧边界的二分搜索

int left_bound(int[] nums, int target) {
    int left = 0;
    int right = nums.length; // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

寻找右侧边界的二分查找

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意

逻辑统一

有了搜索左右边界的二分搜索，你可以去解决力扣第 34 题「 在排序数组中查找元素的第一个和最后一个位置」，

接下来梳理一下这些细节差异的因果逻辑：

第一个，最基本的二分查找算法：

因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1

因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid

因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界

又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right，必须减一

对于寻找左右边界的二分搜索，常见的手法是使用左闭右开的「搜索区间」，我们还根据逻辑将「搜索区间」全都统一成了两端都闭，便于记忆，只要修改两处即可变化出三种写法：

int binary_search(int[] nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // 此时 target 比所有数都大，返回 -1
    if (left == nums.length) return -1;
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
}

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 此时 left - 1 索引越界
    if (left - 1 < 0) return -1;
    // 判断一下 nums[left] 是不是 target
    return nums[left - 1] == target ? (left - 1) : -1;
}

如果以上内容你都能理解，那么恭喜你，二分查找算法的细节不过如此。通过本文，你学会了：

1、分析二分查找代码时，不要出现 else，全部展开成 else if 方便理解。

2、注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。

3、如需定义左闭右开的「搜索区间」搜索左右边界，只要在 nums[mid] == target 时做修改即可，搜索右侧时需要减一。

4、如果将「搜索区间」全都统一成两端都闭，好记，只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可，推荐拿小本本记下，作为二分搜索模板。

最后我想说，以上二分搜索的框架属于「术」的范畴，如果上升到「道」的层面，二分思维的精髓就是：通过已知信息尽可能多地收缩（折半）搜索空间，从而增加穷举效率，快速找到目标。

二维数组的遍历技巧

文章参考

参考链接：二维数组的花式遍历技巧

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 48：旋转图像
• 54：螺旋矩阵
• 59：螺旋矩阵 II
• 151：反转字符串中的单词
• 剑指 Offer 29：顺时针打印矩阵
• 剑指 Offer 58 - I：翻转单词顺序

最大子数组

文章参考

参考链接：动态规划设计：最大子数组

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 53：最大子数组和
• 剑指 Offer 42：连续子数组的最大和

简单总结下动态规划解法吧，虽然说状态转移方程确实有点玄学，但大部分还是有些规律可循的，跑不出那几个套路。像子数组、子序列这类问题，你就可以尝试定义 dp[i] 是以 nums[i] 为结尾的最大子数组和/最长递增子序列，因为这样定义更容易将 dp[i+1] 和 dp[i] 建立起联系，利用数学归纳法写出状态转移方程。

贪心思想玩跳跃游戏

文章参考

参考链接：如何运用贪心思想玩跳跃游戏

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 45：跳跃游戏 II
• 55：跳跃游戏

动态规划和贪心算法到底有啥关系?

说白了，贪心算法可以理解为一种特殊的动态规划问题，拥有一些更特殊的性质，可以进一步降低动态规划算法的时间复杂度。那么这篇文章，就讲 LeetCode 上两道经典的贪心算法：跳跃游戏 I 和跳跃游戏 II。

不知道读者有没有发现，有关动态规划的问题，大多是让你求最值的，比如最长子序列，最小编辑距离，最长公共子串等等等。这就是规律，因为动态规划本身就是运筹学里的一种求最值的算法。

那么贪心算法作为特殊的动态规划也是一样，也一定是让你求个最值。

解决区间问题

文章参考

参考链接：一文秒杀所有区间相关问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 56：合并区间
• 986：区间列表的交集
• 1288：删除被覆盖区间
• 剑指 Offer II 074：合并区间

所谓区间问题，就是线段问题，让你合并所有线段、找出线段的交集等等。主要有两个技巧：

1、排序。常见的排序方法就是按照区间起点排序，或者先按照起点升序排序，若起点相同，则按照终点降序排序。当然，如果你非要按照终点排序，无非对称操作，本质都是一样的。

2、画图。就是说不要偷懒，勤动手，两个区间的相对位置到底有几种可能，不同的相对位置我们的代码应该怎么去处理。

动态规划套路

动态规划解题套路框架

文章参考

参考链接：动态规划解题套路框架

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 322：零钱兑换
• 509：斐波那契数
• 剑指 Offer II 103：最少的硬币数目

首先，动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列呀，最小编辑距离呀等等。

既然是要求最值，核心问题是什么呢？求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值呗。

动态规划这么简单，就是穷举就完事了？我看到的动态规划问题都很难啊！

首先，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，需要你熟练掌握递归思维，只有列出正确的「状态转移方程」，才能正确地穷举。而且，你需要判断算法问题是否具备「最优子结构」，是否能够通过子问题的最值得到原问题的最值。另外，动态规划问题存在「重叠子问题」，如果暴力穷举的话效率会很低，所以需要你使用「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我总结的一个思维框架，辅助你思考状态转移方程：

明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

按上面的套路走，最后的解法代码就会是如下的框架：

# 自顶向下递归的动态规划
def dp(状态1, 状态2, ...):
    for 选择 in 所有可能的选择:
        # 此时的状态已经因为做了选择而改变
        result = 求最值(result, dp(状态1, 状态2, ...))
    return result

# 自底向上迭代的动态规划
# 初始化 base case
dp[0][0][...] = base case
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

注：如果是自顶向下，一般会有个dp函数来递归，然后使用备忘录优化。如果是自底向上，那么一般有一个dp数组，来填充结果。

动态规划之最小路径和

文章参考

参考链接：动态规划之最小路径和

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 64：最小路径和
• 剑指 Offer II 099：最小路径之和

一般来说，让你在二维矩阵中求最优化问题（最大值或者最小值），肯定需要递归 + 备忘录，也就是动态规划技巧。

经典动态规划：编辑距离

文章参考

参考链接：经典动态规划：编辑距离

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 72：编辑距离

解决两个字符串的动态规划问题，一般都是用两个指针 i, j 分别指向两个字符串的最后，然后一步步往前移动，缩小问题的规模。

动态规划设计：最长递增子序列

文章参考

参考链接：动态规划设计：最长递增子序列

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 300：最长递增子序列
• 354：俄罗斯套娃信封问题

岛屿问题

文章参考

参考链接：一文秒杀所有岛屿题目

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 79：单词搜索
• 200：岛屿数量
• 694：不同岛屿的数量🔒
• 695：岛屿的最大面积
• 1020：飞地的数量
• 1254：统计封闭岛屿的数目
• 1905：统计子岛屿
• 剑指 Offer II 105：岛屿的最大面积

岛屿系列题目的核心考点就是用 DFS/BFS 算法遍历二维数组。

那么如何在二维矩阵中使用 DFS 搜索呢？如果你把二维矩阵中的每一个位置看做一个节点，这个节点的上下左右四个位置就是相邻节点，那么整个矩阵就可以抽象成一幅网状的「图」结构。

根据 学习数据结构和算法的框架思维，完全可以根据二叉树的遍历框架改写出二维矩阵的 DFS 代码框架：

// 二叉树遍历框架
void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
}

// 二维矩阵遍历框架
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引边界
        return;
    }
    if (visited[i][j]) {
        // 已遍历过 (i, j)
        return;
    }
    // 进入节点 (i, j)
    visited[i][j] = true;
    dfs(grid, i - 1, j, visited); // 上
    dfs(grid, i + 1, j, visited); // 下
    dfs(grid, i, j - 1, visited); // 左
    dfs(grid, i, j + 1, visited); // 右
}

二叉树遍历框架

文章参考

参考链接：东哥带你刷二叉树（纲领篇）

参考链接：东哥带你刷二叉树（思路篇）

参考链接：东哥带你刷二叉树（序列化篇） 参考链接：二叉树的题，就那几个框架，枯燥至极🤔

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 94：二叉树的中序遍历
• 104：二叉树的最大深度
• 114：二叉树展开为链表
• 116：填充每个节点的下一个右侧节点指针
• 124：二叉树中的最大路径和
• 144：二叉树的前序遍历
• 145：二叉树的后序遍历
• 226：翻转二叉树
• 250：统计同值子树[VIP]
• 366：寻找二叉树的叶子节点[VIP]
• 543：二叉树的直径
• 687：最长同值路径
• 814：二叉树剪枝
• 979：在二叉树中分配硬币
• 1245：树的直径[VIP]
• 剑指 Offer 27：二叉树的镜像
• 剑指 Offer 55 - I：二叉树的深度
• 剑指 Offer II 047：二叉树剪枝
• 剑指 Offer II 051：节点之和最大的路径
• 297：二叉树的序列化与反序列化
• 剑指 Offer 37：序列化二叉树
• 剑指 Offer II 048：序列化与反序列化二叉树

东哥带你刷二叉树（纲领篇）

举个例子，比如两个经典排序算法 快速排序 和 归并排序，对于它俩，你有什么理解？

如果你告诉我，快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历，那么我就知道你是个算法高手了。

为什么快速排序和归并排序能和二叉树扯上关系？我们来简单分析一下他们的算法思想和代码框架：

快速排序的逻辑是，若要对 nums[lo..hi] 进行排序，我们先找一个分界点 p，通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p]，且 nums[p+1..hi] 都大于 nums[p]，然后递归地去 nums[lo..p-1] 和 nums[p+1..hi] 中寻找新的分界点，最后整个数组就被排序了。

快速排序的代码框架如下：

void sort(int[] nums, int lo, int hi) {
    /****** 前序遍历位置 ******/
    // 通过交换元素构建分界点 p
    int p = partition(nums, lo, hi);
    /************************/

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

先构造分界点，然后去左右子数组构造分界点，你看这不就是一个二叉树的前序遍历吗？

再说说归并排序的逻辑，若要对 nums[lo..hi] 进行排序，我们先对 nums[lo..mid] 排序，再对 nums[mid+1..hi] 排序，最后把这两个有序的子数组合并，整个数组就排好序了。

归并排序的代码框架如下：

// 定义：排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    // 排序 nums[lo..mid]
    sort(nums, lo, mid);
    // 排序 nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    /****** 后序位置 ******/
    // 合并 nums[lo..mid] 和 nums[mid+1..hi]
    merge(nums, lo, mid, hi);
    /*********************/
}

先对左右子数组排序，然后合并（类似合并有序链表的逻辑），你看这是不是二叉树的后序遍历框架？另外，这不就是传说中的分治算法嘛，不过如此呀。

如果你一眼就识破这些排序算法的底细，还需要背这些经典算法吗？不需要。你可以手到擒来，从二叉树遍历框架就能扩展出算法了。

说了这么多，旨在说明，二叉树的算法思想的运用广泛，甚至可以说，只要涉及递归，都可以抽象成二叉树的问题。

东哥带你刷二叉树（思路篇）

本文承接 东哥带你刷二叉树（纲领篇），先复述一下前文总结的二叉树解题总纲：

二叉树解题的思维模式分两类：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

无论使用哪种思维模式，你都需要思考：

如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

二叉搜索树

文章参考

参考链接：东哥带你刷二叉搜索树（特性篇） 参考链接：手把手刷二叉搜索树（第一期）

参考链接：东哥带你刷二叉搜索树（基操篇） 参考链接：手把手刷二叉搜索树（第二期）

参考链接：东哥带你刷二叉搜索树（构造篇） 参考链接：手把手带你刷通二叉搜索树（第三期）

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 1038：从二叉搜索树到更大和树
• 230：二叉搜索树中第K小的元素
• 538：把二叉搜索树转换为累加树
• 剑指 Offer II 054：所有大于等于节点的值之和

• 450：删除二叉搜索树中的节点
• 700：二叉搜索树中的搜索
• 701：二叉搜索树中的插入操作
• 98：验证二叉搜索树

• 95：不同的二叉搜索树 II
• 96：不同的二叉搜索树

二叉搜索树（Binary Search Tree，后文简写 BST）。

东哥带你刷二叉搜索树（特性篇）

首先，BST 的特性大家应该都很熟悉了：

1、对于 BST 的每一个节点 node，左子树节点的值都比 node 的值要小，右子树节点的值都比 node 的值大。

2、对于 BST 的每一个节点 node，它的左侧子树和右侧子树都是 BST。

二叉搜索树并不算复杂，但我觉得它可以算是数据结构领域的半壁江山，直接基于 BST 的数据结构有 AVL 树，红黑树等等，拥有了自平衡性质，可以提供 logN 级别的增删查改效率；还有 B+ 树，线段树等结构都是基于 BST 的思想来设计的。

从做算法题的角度来看 BST，除了它的定义，还有一个重要的性质：BST 的中序遍历结果是有序的（升序）。

也就是说，如果输入一棵 BST，以下代码可以将 BST 中每个节点的值升序打印出来：

void traverse(TreeNode root) {
    if (root == null) return;
    traverse(root.left);
    // 中序遍历代码位置
    print(root.val);
    traverse(root.right);
}

累加树是使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

东哥带你刷二叉搜索树（基操篇）

BST 的基础操作主要依赖「左小右大」的特性，可以在二叉树中做类似二分搜索的操作，寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树：

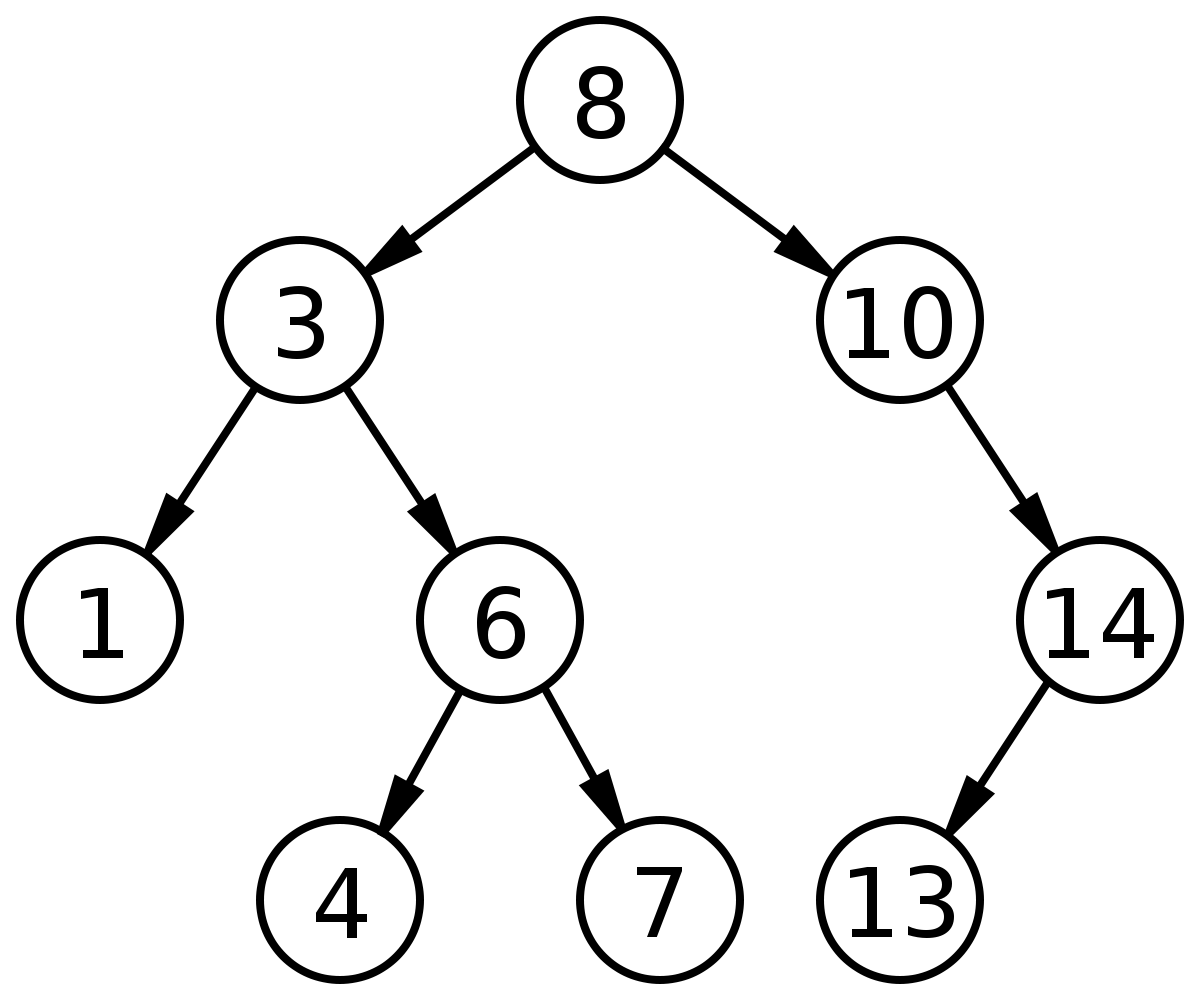
对于 BST 相关的问题，你可能会经常看到类似下面这样的代码逻辑：

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

这个代码框架其实和二叉树的遍历框架差不多，无非就是利用了 BST 左小右大的特性而已。

BST 的每个节点应该要小于右边子树的所有节点

在 BST 中插入一个数:上一个问题，我们总结了 BST 中的遍历框架，就是「找」的问题。直接套框架，加上「改」的操作即可。一旦涉及「改」，就类似二叉树的构造问题，函数要返回 TreeNode 类型，并且要对递归调用的返回值进行接收。

TreeNode insertIntoBST(TreeNode root, int val) {
    // 找到空位置插入新节点
    if (root == null) return new TreeNode(val);
    // if (root.val == val)
    //     BST 中一般不会插入已存在元素
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val);
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val);
    return root;

在 BST 中删除一个数: 这个问题稍微复杂，跟插入操作类似，先「找」再「改」，先把框架写出来再说：

TreeNode deleteNode(TreeNode root, int key) {
    if (root.val == key) {
        // 找到啦，进行删除
    } else if (root.val > key) {
        // 去左子树找
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        // 去右子树找
        root.right = deleteNode(root.right, key);
    }
    return root;
}

找到目标节点了，比方说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，用图片来说明。

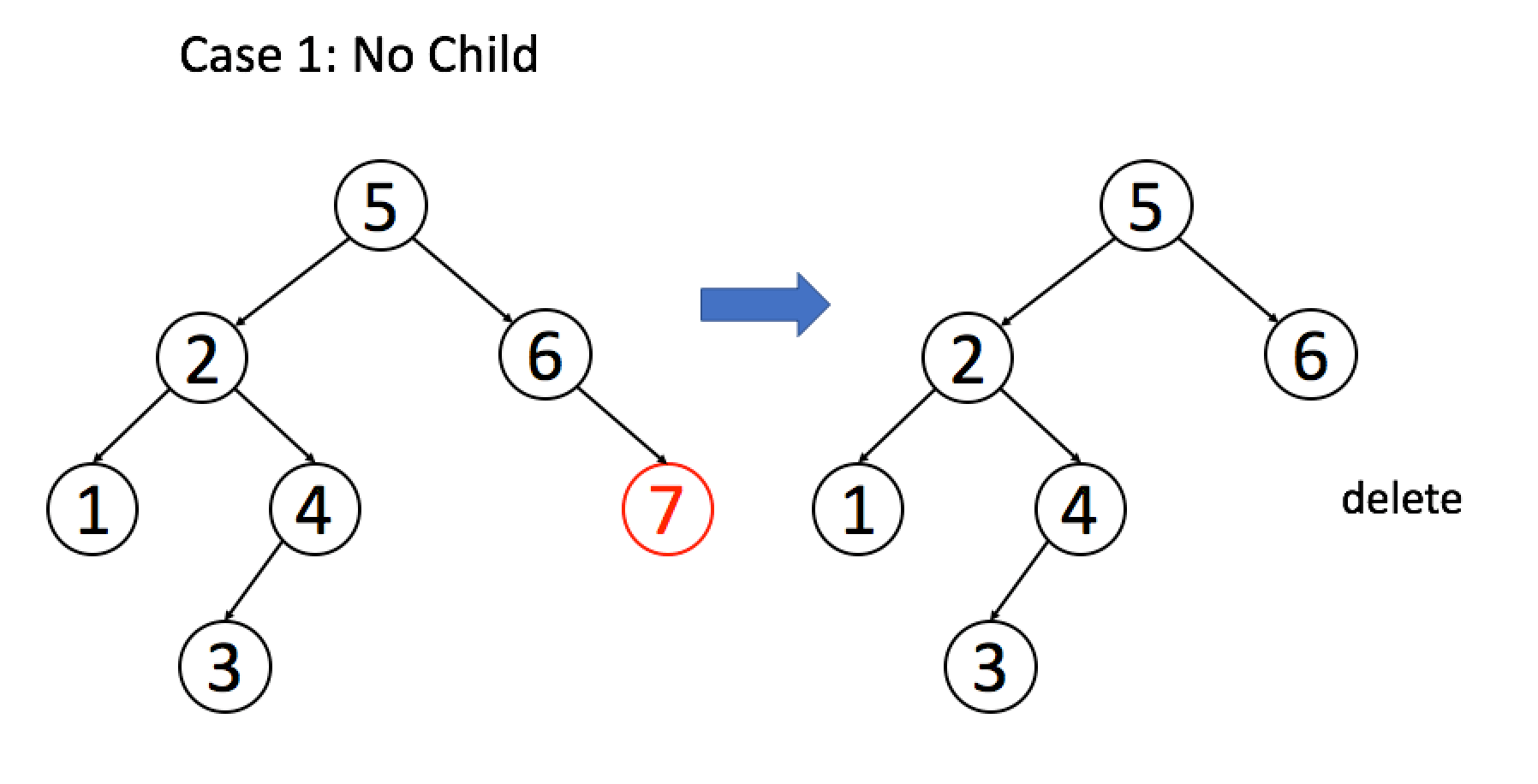
情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了。

if (root.left == null && root.right == null)
    return null;

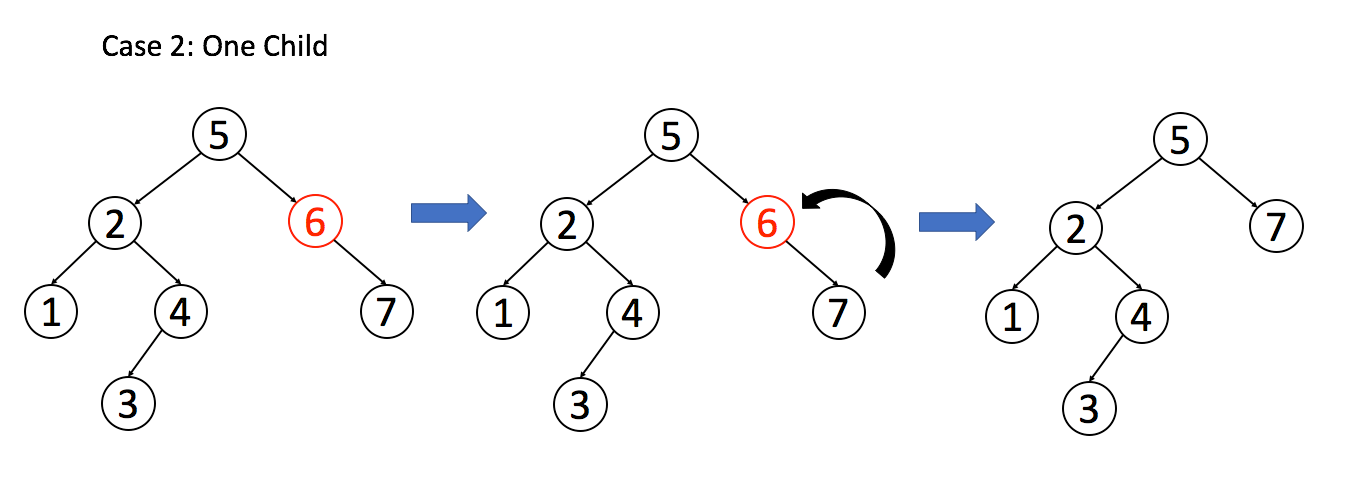
情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。

// 排除了情况 1 之后
if (root.left == null) return root.right;
if (root.right == null) return root.left;

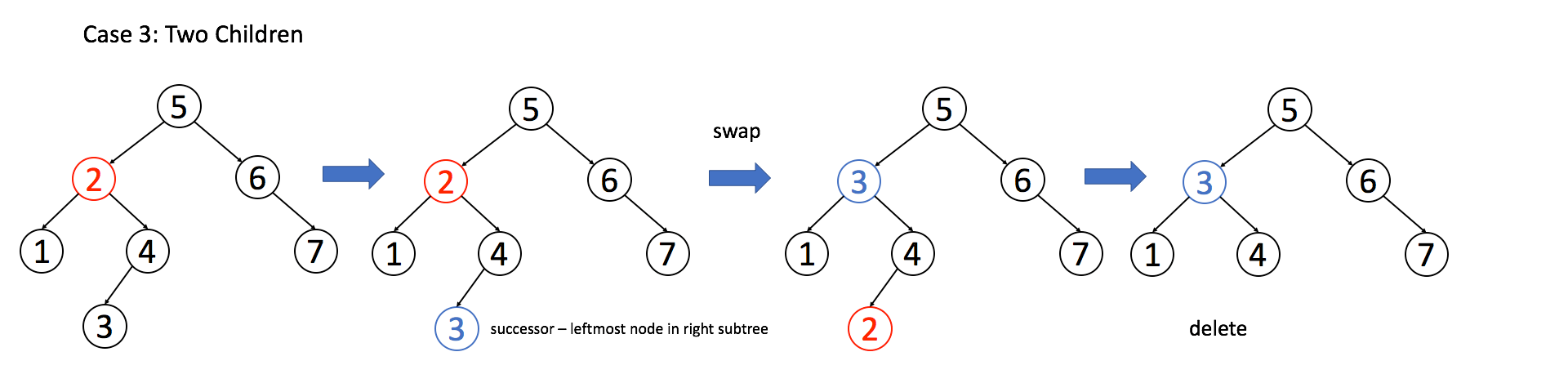
情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。

if (root.left != null && root.right != null) {
    // 找到右子树的最小节点
    TreeNode minNode = getMin(root.right);
    // 把 root 改成 minNode
    root.val = minNode.val;
    // 转而去删除 minNode
    root.right = deleteNode(root.right, minNode.val);
}

三种情况分析完毕，填入框架，简化一下代码：

TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (root.val == key) {
        // 这两个 if 把情况 1 和 2 都正确处理了
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // 处理情况 3
        // 获得右子树最小的节点
        TreeNode minNode = getMin(root.right);
        // 删除右子树最小的节点
        root.right = deleteNode(root.right, minNode.val);
        // 用右子树最小的节点替换 root 节点
        minNode.left = root.left;
        minNode.right = root.right;
        root = minNode;
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

TreeNode getMin(TreeNode node) {
    // BST 最左边的就是最小的
    while (node.left != null) node = node.left;
    return node;
}

这样，删除操作就完成了。注意一下，上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点：

// 处理情况 3
// 获得右子树最小的节点
TreeNode minNode = getMin(root.right);
// 删除右子树最小的节点
root.right = deleteNode(root.right, minNode.val);
// 用右子树最小的节点替换 root 节点
minNode.left = root.left;
minNode.right = root.right;
root = minNode;

BFS遍历框架

文章参考

参考链接：BFS 算法解题套路框架

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 111：二叉树的最小深度

• 752：打开转盘锁

• 剑指 Offer II 109：开密码锁

• 105：从前序与中序遍历序列构造二叉树

• 103：二叉树的锯齿形层序遍历

• 107：二叉树的层序遍历 II

• 637：二叉树的层平均值

• 919：完全二叉树插入器

• 958：二叉树的完全性检验

• 1161：最大层内元素和

• 1302：层数最深叶子节点的和

• 1609：奇偶树

• 剑指 Offer 32 - I：从上到下打印二叉树

• 剑指 Offer 32 - II：从上到下打印二叉树 II

• 剑指 Offer 32 - III：从上到下打印二叉树 III

其实 DFS 算法就是回溯算法

BFS 的核心思想应该不难理解的，就是把一些问题抽象成图，从一个点开始，向四周开始扩散。一般来说，我们写 BFS 算法都是用「队列」这种数据结构，每次将一个节点周围的所有节点加入队列。

BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度可能比 DFS 大很多，至于为什么，我们后面介绍了框架就很容易看出来了.

要说框架的话，我们先举例一下 BFS 出现的常见场景好吧，问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离，这个例子听起来很枯燥，但是 BFS 算法问题其实都是在干这个事儿，把枯燥的本质搞清楚了，再去欣赏各种问题的包装才能胸有成竹嘛。

记住下面这个框架就 OK 了：

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    
    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj()) {
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
            }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

队列 q 就不说了，BFS 的核心数据结构；cur.adj() 泛指 cur 相邻的节点，比如说二维数组中，cur 上下左右四面的位置就是相邻节点；visited 的主要作用是防止走回头路，大部分时候都是必须的，但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited。

1、为什么 BFS 可以找到最短距离，DFS 不行吗？

首先，你看 BFS 的逻辑，depth 每增加一次，队列中的所有节点都向前迈一步，这保证了第一次到达终点的时候，走的步数是最少的。

DFS 不能找最短路径吗？其实也是可以的，但是时间复杂度相对高很多。你想啊，DFS 实际上是靠递归的堆栈记录走过的路径，你要找到最短路径，肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对？而 BFS 借助队列做到一次一步「齐头并进」，是可以在不遍历完整棵树的条件下找到最短距离的。

形象点说，DFS 是线，BFS 是面；DFS 是单打独斗，BFS 是集体行动。这个应该比较容易理解吧。

2、既然 BFS 那么好，为啥 DFS 还要存在？

BFS 可以找到最短距离，但是空间复杂度高，而 DFS 的空间复杂度较低。

还是拿刚才我们处理二叉树问题的例子，假设给你的这个二叉树是满二叉树，节点数为 N，对于 DFS 算法来说，空间复杂度无非就是递归堆栈，最坏情况下顶多就是树的高度，也就是 O(logN)。

但是你想想 BFS 算法，队列中每次都会储存着二叉树一层的节点，这样的话最坏情况下空间复杂度应该是树的最底层节点的数量，也就是 N/2，用 Big O 表示的话也就是 O(N)。

由此观之，BFS 还是有代价的，一般来说在找最短路径的时候使用 BFS，其他时候还是 DFS 使用得多一些（主要是递归代码好写）。

好了，现在你对 BFS 了解得足够多了，下面来一道难一点的题目，深化一下框架的理解吧。

BFS 算法还有一种稍微高级一点的优化思路：双向 BFS，可以进一步提高算法的效率。

篇幅所限，这里就提一下区别：传统的 BFS 框架就是从起点开始向四周扩散，遇到终点时停止；而双向 BFS 则是从起点和终点同时开始扩散，当两边有交集的时候停止。

不过，双向 BFS 也有局限，因为你必须知道终点在哪里。

不过话说回来，无论传统 BFS 还是双向 BFS，无论做不做优化，从 Big O 衡量标准来看，时间复杂度都是一样的，只能说双向 BFS 是一种 trick，算法运行的速度会相对快一点，掌握不掌握其实都无所谓。最关键的是把 BFS 通用框架记下来，反正所有 BFS 算法都可以用它套出解法。

股票买卖问题

文章参考

参考链接：一个方法团灭 LEETCODE 股票买卖问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 121：买卖股票的最佳时机
• 122：买卖股票的最佳时机 II
• 123：买卖股票的最佳时机 III
• 188：买卖股票的最佳时机 IV
• 309：最佳买卖股票时机含冷冻期
• 714：买卖股票的最佳时机含手续费
• 剑指 Offer 63：股票的最大利润

首先，还是一样的思路：如何穷举？

动态规划核心套路 说过，动态规划算法本质上就是穷举「状态」，然后在「选择」中选择最优解。

这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：

dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n 为天数，大 K 为交易数的上限，0 和 1 代表是否持有股票。
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

而且我们可以用自然语言描述出每一个状态的含义，比如说 dp[3][2][1] 的含义就是：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义：今天是第二天，我现在手上没有持有股票，至今最多进行 3 次交易。很容易理解，对吧？

我们想求的最终答案是 dp[n - 1][K][0]，即最后一天，最多允许 K 次交易，最多获得多少利润。

读者可能问为什么不是 dp[n - 1][K][1]？因为 dp[n - 1][K][1] 代表到最后一天手上还持有股票，dp[n - 1][K][0] 表示最后一天手上的股票已经卖出去了，很显然后者得到的利润一定大于前者。

记住如何解释「状态」，一旦你觉得哪里不好理解，把它翻译成自然语言就容易理解了。

现在，我们完成了「状态」的穷举，我们开始思考每种「状态」有哪些「选择」，应该如何更新「状态」。

只看「持有状态」，可以画个状态转移图：

通过这个图可以很清楚地看到，每种状态（0 和 1）是如何转移而来的。根据这个图，我们来写一下状态转移方程：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( 今天选择 rest,        今天选择 sell       )

解释：今天我没有持有股票，有两种可能，我从这两种可能中求最大利润：

1、我昨天就没有持有，且截至昨天最大交易次数限制为 k；然后我今天选择 rest，所以我今天还是没有持有，最大交易次数限制依然为 k。

2、我昨天持有股票，且截至昨天最大交易次数限制为 k；但是今天我 sell 了，所以我今天没有持有股票了，最大交易次数限制依然为 k。

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( 今天选择 rest,         今天选择 buy         )

解释：今天我持有着股票，最大交易次数限制为 k，那么对于昨天来说，有两种可能，我从这两种可能中求最大利润：

1、我昨天就持有着股票，且截至昨天最大交易次数限制为 k；然后今天选择 rest，所以我今天还持有着股票，最大交易次数限制依然为 k。

2、我昨天本没有持有，且截至昨天最大交易次数限制为 k - 1；但今天我选择 buy，所以今天我就持有股票了，最大交易次数限制为 k。

这里着重提醒一下，时刻牢记「状态」的定义，状态 k 的定义并不是「已进行的交易次数」，而是「最大交易次数的上限限制」。如果确定今天进行一次交易，且要保证截至今天最大交易次数上限为 k，那么昨天的最大交易次数上限必须是 k - 1。

这个解释应该很清楚了，如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。

注意 k 的限制，在选择 buy 的时候相当于开启了一次交易，那么对于昨天来说，交易次数的上限 k 应该减小 1。

修正：以前我以为在 sell 的时候给 k 减小 1 和在 buy 的时候给 k 减小 1 是等效的，但细心的读者向我提出质疑，经过深入思考我发现前者确实是错误的，因为交易是从 buy 开始，如果 buy 的选择不改变交易次数 k 的话，会出现交易次数超出限制的的错误。

现在，我们已经完成了动态规划中最困难的一步：状态转移方程。如果之前的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就行了。不过还差最后一点点，就是定义 base case，即最简单的情况。

dp[-1][...][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0。

dp[-1][...][1] = -infinity
解释：还没开始的时候，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

dp[...][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0。

dp[...][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的。
因为我们的算法要求一个最大值，所以初始值设为一个最小值，方便取最大值。

把上面的状态转移方程总结一下：

base case：
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

读者可能会问，这个数组索引是 -1 怎么编程表示出来呢，负无穷怎么表示呢？这都是细节问题，有很多方法实现。现在完整的框架已经完成，下面开始具体化。

常用的位操作

文章参考

参考链接：常用的位操作

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 136：只出现一次的数字
• 191：位1的个数
• 231：2 的幂
• 268：丢失的数字
• 剑指 Offer 15：二进制中1的个数

使用的运算符包括下面：

含义	运算符	例子	备注
左移	<<	0011 => 0110	所有位往左移动
右移	>>	0110 => 0011	所有位往右移动
按位或	︳	0011 ------- => 1011 1011	位有一个1就为1，否则为0
按位与	&	0011 ------- => 0011 1011	位都是1才是1，否则为0
按位取反	~	0011 => 1100	每个位置取反
按位异或 (相同为零不同为一)	^	0011 ------- => 1000 1011	两个位置相同为0，不一样为1
按位右移补零操作符，移动得到的空位用0填充	>>>	4 >>>1 =2	第二个数字是向右移动几位

异或运算 XOR，主要因为异或运算有以下几个特点：

一个数和 0 做 XOR 运算等于本身：a⊕0 = a

一个数和其本身做 XOR 运算等于 0：a⊕a = 0

XOR 运算满足交换律和结合律：a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b

一个数和它本身做异或运算结果为 0，即 a ^ a = 0；一个数和 0 做异或运算的结果为它本身，即 a ^ 0 = a。

几个有趣的位操作

利用或操作 | 和空格将英文字符转换为小写

('a' | ' ') = 'a'
('A' | ' ') = 'a'

利用与操作 & 和下划线将英文字符转换为大写

('b' & '_') = 'B'
('B' & '_') = 'B'

利用异或操作 ^ 和空格进行英文字符大小写互换

('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'

以上操作能够产生奇特效果的原因在于 ASCII 编码。ASCII 字符其实就是数字，恰巧空格和下划线对应的数字通过位运算就能改变大小写。有兴趣的读者可以查 ASCII 码表自己算算，本文就不展开讲了。

不用临时变量交换两个数

int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1

加一

int n = 1;
n = -~n;
// 现在 n = 2

减一

int n = 2;
n = ~-n;
// 现在 n = 1

判断两个数是否异号

int x = -1, y = 2;
boolean f = ((x ^ y) < 0); // true

int x = 3, y = 2;
boolean f = ((x ^ y) < 0); // false

如果说前 6 个技巧的用处不大，这第 7 个技巧还是比较实用的，利用的是补码编码的符号位。整数编码最高位是符号位，负数的符号位是 1，非负数的符号位是 0，再借助异或的特性，可以判断出两个数字是否异号。

当然，如果不用位运算来判断是否异号，需要使用 if else 分支，还挺麻烦的。你可能想利用乘积来判断两个数是否异号，但是这种处理方式容易造成整型溢出，从而出现错误。

---

反转单链表

文章参考

参考链接：递归魔法：反转单链表

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 206：反转链表
• 92：反转链表 II
• 剑指 Offer 24：反转链表
• 剑指 Offer II 024：反转链表

// 定义：输入一个单链表头结点，将该链表反转，返回新的头结点
ListNode reverse(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

看起来是不是感觉不知所云，完全不能理解这样为什么能够反转链表？这就对了，这个算法常常拿来显示递归的巧妙和优美，我们下面来详细解释一下这段代码。

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

输入一个节点 head，将「以 head 为起点」的链表反转，并返回反转之后的头结点。

回文链表

文章参考

参考链接：如何判断回文链表

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 234：回文链表
• 剑指 Offer II 027：回文链表

寻找回文串的核心思想是从中心向两端扩展：

// 在 s 中寻找以 s[left] 和 s[right] 为中心的最长回文串
String palindrome(String s, int left, int right) {
    // 防止索引越界
    while (left >= 0 && right < s.length()
            && s.charAt(left) == s.charAt(right)) {
        // 双指针，向两边展开
        left--;
        right++;
    }
    // 返回以 s[left] 和 s[right] 为中心的最长回文串
    return s.substring(left + 1, right);
}

因为回文串长度可能为奇数也可能是偶数，长度为奇数时只存在一个中心点，而长度为偶数时存在两个中心点，所以上面这个函数需要传入 l 和 r。

而判断一个字符串是不是回文串就简单很多，不需要考虑奇偶情况，只需要 双指针技巧，从两端向中间逼近即可：

boolean isPalindrome(String s) {
    // 一左一右两个指针相向而行
    int left = 0, right = s.length() - 1;
    while (left < right) {
        if (s.charAt(left) != s.charAt(right)) {
            return false;
        }
        left++;
        right--;
    }
    return true;
}

以上代码很好理解吧，因为回文串是对称的，所以正着读和倒着读应该是一样的，这一特点是解决回文串问题的关键。

单词拼接问题

文章参考

参考链接：高频面试系列：单词拆分问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 139 ：单词拆分
• 剑指 Offer II 027：回文链表

前文 动态规划核心框架详解 说，标准的动态规划问题一定是求最值的，因为动态规划类型问题有一个性质叫做「最优子结构」，即从子问题的最优解推导出原问题的最优解。

但在我们平常的语境中，就算不是求最值的题目，只要看见使用备忘录消除重叠子问题，我们一般都称它为动态规划算法。严格来讲这是不符合动态规划问题的定义的，说这种解法叫做「带备忘录的 DFS 算法」可能更准确些。不过咱也不用太纠结这种名词层面的细节，既然大家叫的顺口，就叫它动态规划也无妨。

先说说「遍历」的思路，也就是用回溯算法解决本题。回溯算法最经典的应用就是排列组合相关的问题了

LRU(Least Recently Used)缓存淘汰算法

文章参考

参考链接：算法就像搭乐高：带你手撸 LRU 算法

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 146：LRU 缓存
• 剑指 Offer II 031：最近最少使用缓存

LRU 算法就是一种缓存淘汰策略，原理不难，但是面试中写出没有 bug 的算法比较有技巧，需要对数据结构进行层层抽象和拆解，本文就带你写一手漂亮的代码。

计算机的缓存容量有限，如果缓存满了就要删除一些内容，给新内容腾位置。但问题是，删除哪些内容呢？我们肯定希望删掉哪些没什么用的缓存，而把有用的数据继续留在缓存里，方便之后继续使用。那么，什么样的数据，我们判定为「有用的」的数据呢？

LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently Used，也就是说我们认为最近使用过的数据应该是是「有用的」，很久都没用过的数据应该是无用的，内存满了就优先删那些很久没用过的数据。

打家劫舍问题

文章参考

参考链接：一个方法团灭 LEETCODE 打家劫舍问题

参考链接：经典动态规划：打家劫舍系列问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 198：打家劫舍
• 213：打家劫舍 II
• 337：House Robber III
• 剑指 Offer II 089：房屋偷盗
• 剑指 Offer II 090：环形房屋偷盗

图的遍历

文章参考

参考链接：图论基础及遍历算法

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 797：所有可能的路径
• 剑指 Offer II 110：所有路径

一幅图是由节点和边构成的，逻辑结构如下：

什么叫「逻辑结构」？就是说为了方便研究，我们把图抽象成这个样子。

根据这个逻辑结构，我们可以认为每个节点的实现如下：

/* 图节点的逻辑结构 */
class Vertex {
    int id;
    Vertex[] neighbors;
}

看到这个实现，你有没有很熟悉？它和我们之前说的多叉树节点几乎完全一样：

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

所以说，图真的没啥高深的，本质上就是个高级点的多叉树而已，适用于树的 DFS/BFS 遍历算法，全部适用于图。

不过呢，上面的这种实现是「逻辑上的」，实际上我们很少用这个 Vertex 类实现图，而是用常说的邻接表和邻接矩阵来实现。

比如还是刚才那幅图：

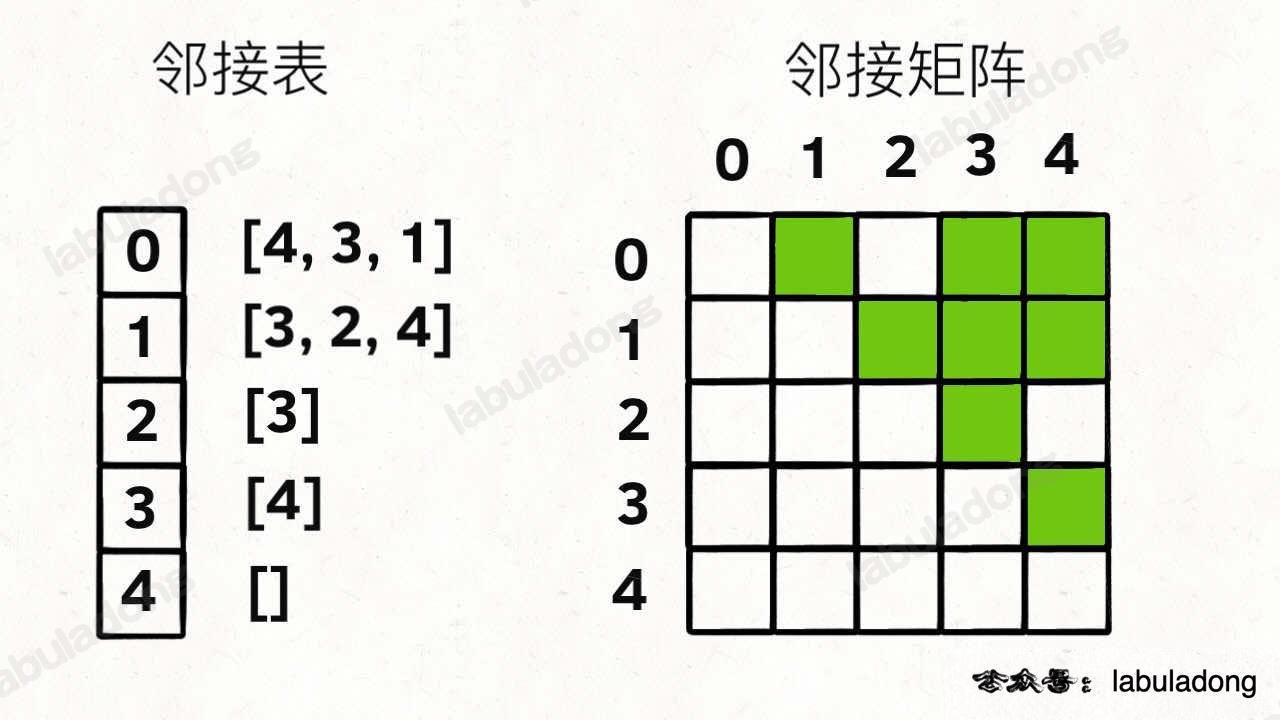
用邻接表和邻接矩阵的存储方式如下：

邻接表很直观，我把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表关联起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

邻接矩阵则是一个二维布尔数组，我们权且称为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][..] 就行了。

如果用代码的形式来表现，邻接表和邻接矩阵大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

那么，为什么有这两种存储图的方式呢？肯定是因为他们各有优劣。

对于邻接表，好处是占用的空间少。

你看邻接矩阵里面空着那么多位置，肯定需要更多的存储空间。

但是，邻接表无法快速判断两个节点是否相邻。

比如说我想判断节点 1 是否和节点 3 相邻，我要去邻接表里 1 对应的邻居列表里查找 3 是否存在。但对于邻接矩阵就简单了，只要看看 matrix[1][3] 就知道了，效率高。

所以说，使用哪一种方式实现图，要看具体情况。

PS：在常规的算法题中，邻接表的使用会更频繁一些，主要是因为操作起来较为简单，但这不意味着邻接矩阵应该被轻视。矩阵是一个强有力的数学工具，图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容，所以有兴趣的读者可以自行搜索学习。

最后，我们再明确一个图论中特有的度（degree）的概念，在无向图中，「度」就是每个节点相连的边的条数。

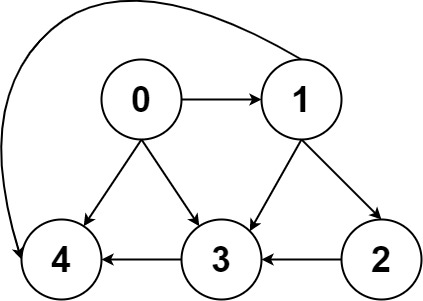
由于有向图的边有方向，所以有向图中每个节点「度」被细分为入度（indegree）和出度（outdegree），比如下图：

其中节点 3 的入度为 3（有三条边指向它），出度为 1（它有 1 条边指向别的节点）。

好了，对于「图」这种数据结构，能看懂上面这些就绰绰够用了。

那你可能会问，我们上面说的这个图的模型仅仅是「有向无权图」，不是还有什么加权图，无向图，等等……

其实，这些更复杂的模型都是基于这个最简单的图衍生出来的。

有向加权图怎么实现？很简单呀：

如果是邻接表，我们不仅仅存储某个节点 x 的所有邻居节点，还存储 x 到每个邻居的权重，不就实现加权有向图了吗？

如果是邻接矩阵，matrix[x][y] 不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重，不就变成加权有向图了吗？

如果用代码的形式来表现，大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
List<int[]>[] graph;

// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
int[][] matrix;

无向图怎么实现？也很简单，所谓的「无向」，是不是等同于「双向」？

如果连接无向图中的节点 x 和 y，把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了；邻接表也是类似的操作，在 x 的邻居列表里添加 y，同时在 y 的邻居列表里添加 x。

把上面的技巧合起来，就变成了无向加权图……

好了，关于图的基本介绍就到这里，现在不管来什么乱七八糟的图，你心里应该都有底了。

下面来看看所有数据结构都逃不过的问题：遍历。

图怎么遍历？还是那句话，参考多叉树，多叉树的 DFS 遍历框架如下：

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;
    // 前序位置
    for (TreeNode child : root.children) {
        traverse(child);
    }
    // 后序位置
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点，而树不会出现这种情况，从某个节点出发必然走到叶子节点，绝不可能回到它自身。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

注意 visited 数组和 onPath 数组的区别，因为二叉树算是特殊的图，所以用遍历二叉树的过程来理解下这两个数组的区别：

他们的区别可以这样反应到代码上：

// DFS 算法，关注点在节点
void traverse(TreeNode root) {
    if (root == null) return;
    printf("进入节点 %s", root);
    for (TreeNode child : root.children) {
        traverse(child);
    }
    printf("离开节点 %s", root);
}

// 回溯算法，关注点在树枝
void backtrack(TreeNode root) {
    if (root == null) return;
    for (TreeNode child : root.children) {
        // 做选择
        printf("从 %s 到 %s", root, child);
        backtrack(child);
        // 撤销选择
        printf("从 %s 到 %s", child, root);
    }
}

如果执行这段代码，你会发现根节点被漏掉了：

环检测及拓扑排序算法

文章参考

参考链接：环检测及拓扑排序算法

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 207：课程表
• 210：课程表 II
• 剑指 Offer II 113：课程顺序

前缀树

文章参考

参考链接：前缀树算法模板秒杀五道算法题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 1804：实现 Trie （前缀树） II🔒
• 208：实现 Trie (前缀树)
• 211：添加与搜索单词 - 数据结构设计
• 648：单词替换
• 677：键值映射
• 剑指 Offer II 062：实现前缀树
• 剑指 Offer II 063：替换单词
• 剑指 Offer II 066：单词之和

Trie 树又叫字典树、前缀树、单词查找树，是一种二叉树衍生出来的高级数据结构，主要应用场景是处理字符串前缀相关的操作。

本文主要分三部分：

1、讲解 Trie 树的工作原理。

2、给出一套 TrieMap 和 TrieSet 的代码模板，实现几个常用 API。

3、实践环节，直接套代码模板秒杀 5 道算法题。本来可以秒杀七八道题，篇幅考虑，剩下的我集成到 刷题插件 中。

关于 Map 和 Set，是两个抽象数据结构（接口），Map 存储一个键值对集合，其中键不重复，Set 存储一个不重复的元素集合。

常见的 Map 和 Set 的底层实现原理有哈希表和二叉搜索树两种，比如 Java 的 HashMap/HashSet 和 C++ 的 unorderd_map/unordered_set 底层就是用哈希表实现，而 Java 的 TreeMap/TreeSet 和 C++ 的 map/set 底层使用红黑树这种自平衡 BST 实现的。

而本文实现的 TrieSet/TrieMap 底层则用 Trie 树这种结构来实现。

了解数据结构的读者应该知道，本质上 Set 可以视为一种特殊的 Map，Set 其实就是 Map 中的键。

所以本文先实现 TrieMap，然后在 TrieMap 的基础上封装出 TrieSet。

你比如HashMap<K, V>的优势是能够在 O(1) 时间通过键查找对应的值，但要求键的类型K必须是「可哈希」的；而TreeMap<K, V>的特点是方便根据键的大小进行操作，但要求键的类型K必须是「可比较」的。

本文要实现的TrieMap也是类似的，由于 Trie 树原理，我们要求TrieMap<V>的键必须是字符串类型，值的类型V可以随意。

接下来我们了解一下 Trie 树的原理，看看为什么这种数据结构能够高效操作字符串。

Trie 树原理

Trie 树本质上就是一棵从二叉树衍生出来的多叉树。

二叉树节点的代码实现是这样：

/* 基本的二叉树节点 */
class TreeNode {
    int val;
    TreeNode left, right;
}

其中left, right存储左右子节点的指针，所以二叉树的结构是这样：

多叉树节点的代码实现是这样：

/* 基本的多叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

其中children数组中存储指向孩子节点的指针，所以多叉树的结构是这样：

而TrieMap中的树节点TrieNode的代码实现是这样：

/* Trie 树节点实现 */
class TrieNode<V> {
    V val = null;
    TrieNode<V>[] children = new TrieNode[256];
}

这个val字段存储键对应的值，children数组存储指向子节点的指针。

但是和之前的普通多叉树节点不同，TrieNode中children数组的索引是有意义的，代表键中的一个字符。

比如说children[97]如果非空，说明这里存储了一个字符'a'，因为'a'的 ASCII 码为 97。

我们的模板只考虑处理 ASCII 字符，所以children数组的大小设置为 256。不过这个可以根据具体问题修改，比如改成更小的数组或者HashMap<Character, TrieNode>都是一样的效果。

有了以上铺垫，Trie 树的结构是这样的：

一个节点有 256 个子节点指针，但大多数时候都是空的，可以省略掉不画，所以一般你看到的 Trie 树长这样：

这是在TrieMap<Integer>中插入一些键值对后的样子，白色节点代表val字段为空，橙色节点代表val字段非空。

这里要特别注意，TrieNode节点本身只存储val字段，并没有一个字段来存储字符，字符是通过子节点在父节点的children数组中的索引确定的。

形象理解就是，Trie 树用「树枝」存储字符串（键），用「节点」存储字符串（键）对应的数据（值）。所以我在图中把字符标在树枝，键对应的值val标在节点上：

明白这一点很重要，有助于之后你理解代码实现。

PS：《算法 4》以及网上讲 Trie 树的很多文章中都是把字符标在节点上，我认为这样很容易让初学者产生误解，所以建议大家按照我的这种理解来记忆 Trie 树结构。

现在你应该知道为啥 Trie 树也叫前缀树了，因为其中的字符串共享前缀，相同前缀的字符串集中在 Trie 树中的一个子树上，给字符串的处理带来很大的便利。

快速排序

文章参考

参考链接：快速排序详解及应用

参考链接：快速排序的正确理解方式及运用

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 215：数组中的第K个最大元素
• 912：排序数组

首先我们看一下快速排序的代码框架：

void sort(int[] nums, int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);
    // 去左右子数组进行切分
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

其实你对比之后可以发现，快速排序就是一个二叉树的前序遍历：

另外，前文 归并排序详解 用一句话总结了归并排序：先把左半边数组排好序，再把右半边数组排好序，然后把两半数组合并。

同时我提了一个问题，让你一句话总结快速排序，这里说一下我的答案：

快速排序是先将一个元素排好序，然后再将剩下的元素排好序。

最近公共祖先

文章参考

参考链接：GIT原理之最近公共祖先

参考链接：一文秒杀 5 道最近公共祖先问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 1644：二叉树的最近公共祖先 II🔒
• 1650：二叉树的最近公共祖先 III🔒
• 1676：二叉树的最近公共祖先 IV🔒
• 235：二叉搜索树的最近公共祖先
• 236：二叉树的最近公共祖先
• 剑指 Offer 68 - I：二叉搜索树的最近公共祖先
• 剑指 Offer 68 - II：二叉树的最近公共祖先

最近公共祖先（Lowest Common Ancestor，简称 LCA）。

// 定义：在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
TreeNode find(TreeNode root, int val1, int val2) {
    // base case
    if (root == null) {
        return null;
    }
    // 前序位置，看看 root 是不是目标值
    if (root.val == val1 || root.val == val2) {
        return root;
    }
    // 去左右子树寻找
    TreeNode left = find(root.left, val1, val2);
    TreeNode right = find(root.right, val1, val2);
    // 后序位置，已经知道左右子树是否存在目标值

    return left != null ? left : right;
}

为什么要写这样一个奇怪的find函数呢？因为最近公共祖先系列问题的解法都是把这个函数作为框架的。

经典动态规划：戳气球

文章参考

参考链接：经典动态规划：戳气球

参考链接：经典动态规划：戳气球问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 312：戳气球

并查集

文章参考

参考链接：并查集（UNION-FIND）算法

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 130：被围绕的区域
• 323：无向图中连通分量的数目🔒
• 990：等式方程的可满足性

并查集（Union-Find）算法是一个专门针对「动态连通性」的算法

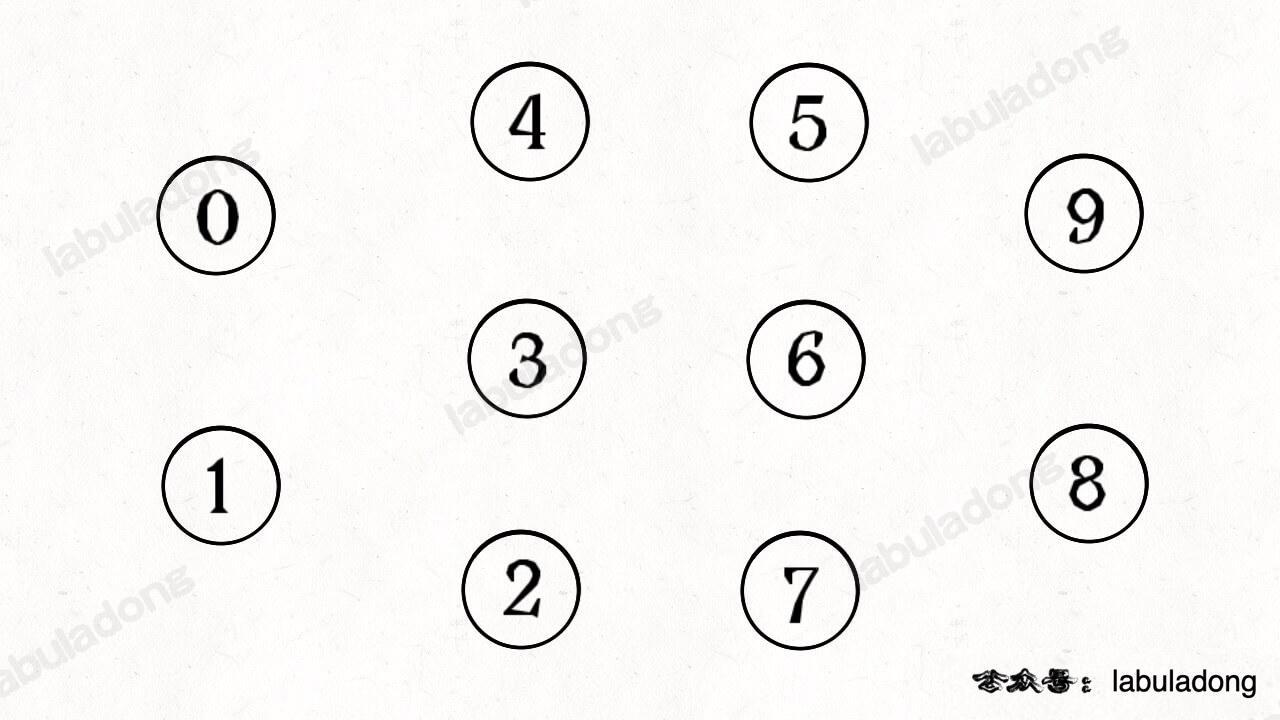
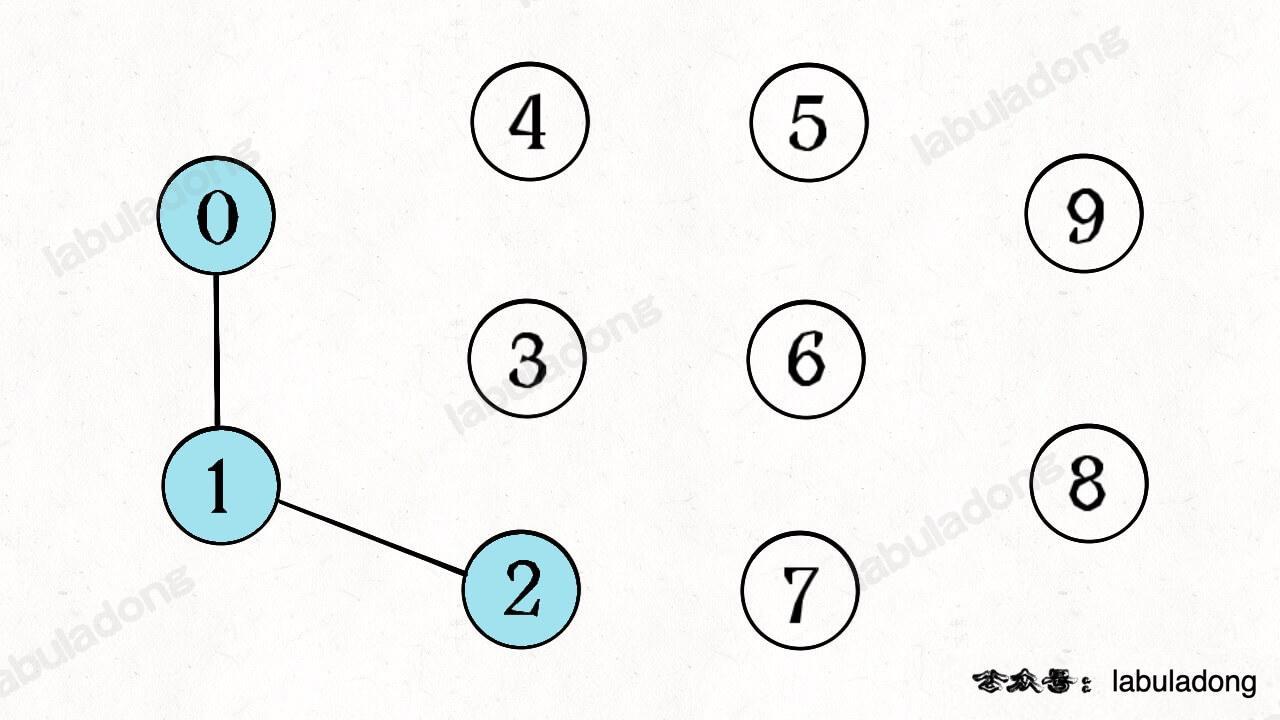
简单说，动态连通性其实可以抽象成给一幅图连线。比如下面这幅图，总共有 10 个节点，他们互不相连，分别用 0~9 标记：

现在我们的 Union-Find 算法主要需要实现这两个 API：

class UF {
    /* 将 p 和 q 连接 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    public boolean connected(int p, int q);
    /* 返回图中有多少个连通分量 */
    public int count();
}

这里所说的「连通」是一种等价关系，也就是说具有如下三个性质：

1、自反性：节点 p 和 p 是连通的。

2、对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。

3、传递性：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。

比如说之前那幅图，0～9 任意两个不同的点都不连通，调用 connected 都会返回 false，连通分量为 10 个。

如果现在调用 union(0, 1)，那么 0 和 1 被连通，连通分量降为 9 个。

再调用 union(1, 2)，这时 0,1,2 都被连通，调用 connected(0, 2) 也会返回 true，连通分量变为 8 个。

判断这种「等价关系」非常实用，比如说编译器判断同一个变量的不同引用，比如社交网络中的朋友圈计算等等。

这样，你应该大概明白什么是动态连通性了，Union-Find 算法的关键就在于 union 和 connected 函数的效率。那么用什么模型来表示这幅图的连通状态呢？用什么数据结构来实现代码呢？

class UF {
    // 连通分量个数
    private int count;
    // 存储每个节点的父节点
    private int[] parent;

    // n 为图中节点的个数
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    
    // 将节点 p 和节点 q 连通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        
        if (rootP == rootQ)
            return;
        
        parent[rootQ] = rootP;
        // 两个连通分量合并成一个连通分量
        count--;
    }

    // 判断节点 p 和节点 q 是否连通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 返回图中的连通分量个数
    public int count() {
        return count;
    }
}

class UnionFind {
        parent: number[];
        count: number;

        constructor(n: number) {
            this.parent = new Array(n);
            this.count = 0;
            for (let i = 0; i < n; i++) {
                this.parent[i] = i;

            }
        }

        union(x: number, y: number) {
            let parentX = this.find(x);
            let parentY = this.find(y);
            if (parentX !== parentY) {
                this.parent[parentX] = parentY
                this.count--;
            }

        }

        find(val: number): number {
            if (val !== this.parent[val]) {
                this.parent[val] = this.find(this.parent[val]);
            }
            return this.parent[val];
        }

        connted(x: number, y: number) {
            return this.find(x) === this.find(y);
        }
    
        get count(){
            return this.count;
        }
    }

经典动态规划：子集背包问题

文章参考

参考链接：经典动态规划：子集背包问题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 416：分割等和子集
• 剑指 Offer II 101：分割等和子集

动态规划和回溯算法到底谁是谁爹？

文章参考

参考链接：动态规划和回溯算法到底谁是谁爹？

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 494：目标和
• 剑指 Offer II 102：加减的目标值

单调栈结构解决三道算法题

文章参考

参考链接：单调栈结构解决三道算法题

著作权归原作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

类似题号：

• 496：下一个更大元素 I
• 503：下一个更大元素 II
• 739：每日温度
• 剑指 Offer II 038：每日温度