前言
前两天,有位前同事和我说他去面试,面试官第一个问题就是问了原码反码补码的的概念和负数的二进制转换原理。他说他工作之后,这些底层原理太久没复习。只能记个大概。回答的不是很清晰。
仔细想想,好像自己的也快忘了。
所以现在,复习一下。
当然,这篇文章也适合初入计算机的同学和跨专业学习的小伙伴。文中关于二进制的描述以一个字节(八位)为基准。
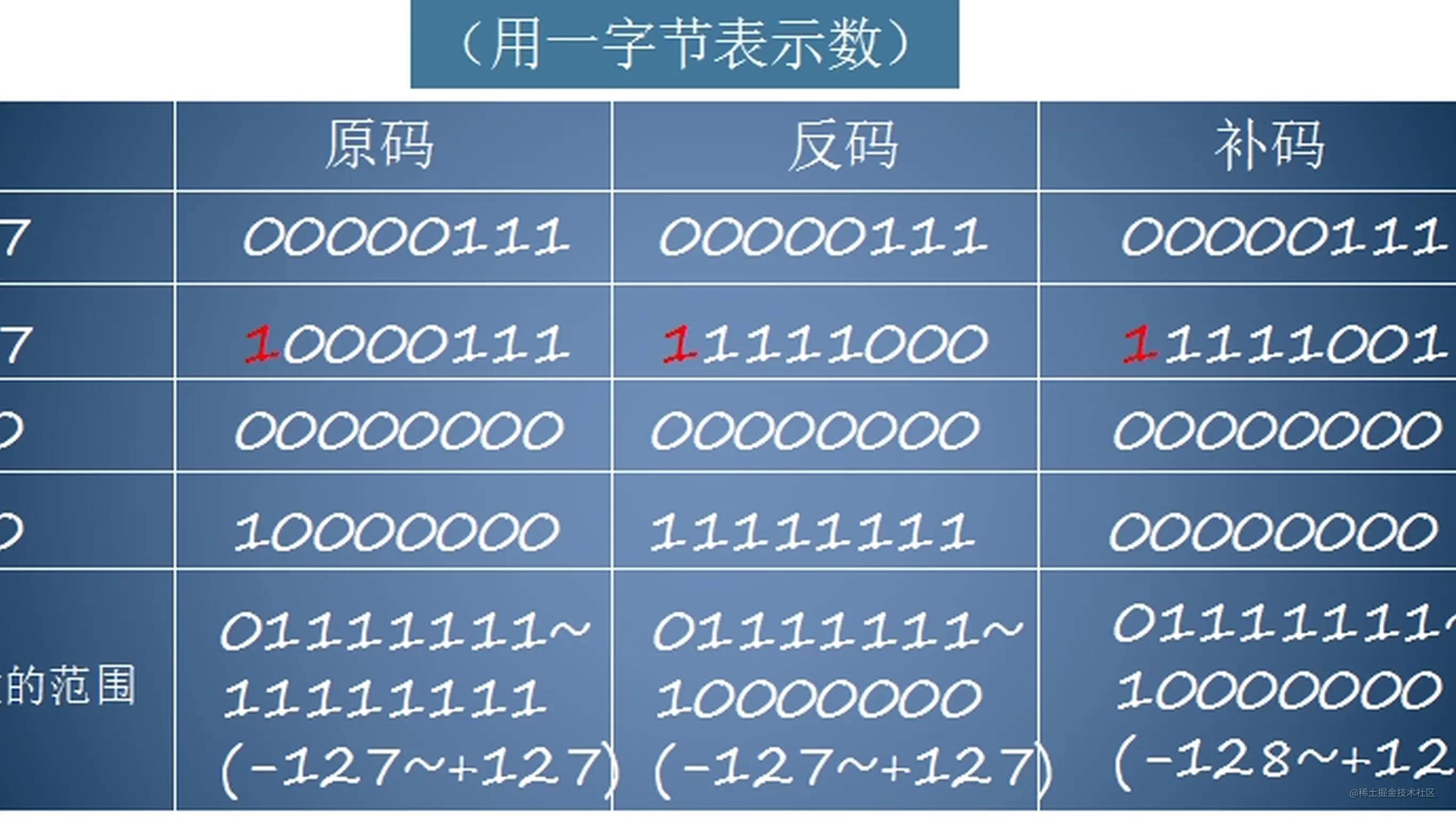
原码,反码,补码到底是什么?
首先,我们需要了解。数字有进制这么一个说法。我们日常生活中的1,2,3,4...也就是被我们称为阿拉伯数字的这些数字,叫十进制数字。
但我们的计算机无法直接存储十进制数字。计算机中只能存储二进制数字。我们在计算机中所看见的一切都是通过二进制数字转化而来的。
所以,什么是二进制数字?
官方回答:二进制是计算技术中广泛采用的一种数制。二进制数字是用 0 和 1 两个数码来表示的数。它的基数为 2,进位规则是“逢二进一”,借位规则是“借一当二”,由 18 世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统。 20 世纪被称作第三次科技革命的重要标志之一的计算机的发明与应用,其运算模式正是二进制,同时证明了莱布尼兹的原理是正确的。
翻译一下就是:二进制是只有 0 和 1 组成的数字。比如 :01011011 (二进制);
二进制和十进制有什么区别?
十进制拥有:0,1,2,3,4,5,6,7,8,9 这十个数字(因为有十个基本数所以他叫 10 进制)
二进制拥有: 0,1 这两个数字。(因为只有两个基本数,所以他叫二进制)
看,很直观,位数种类只有 2 种的叫做二进制。位数种类有十种的叫做十进制。
并且十进制无法被计算机直接存储,但是二进制可以被计算机存储。(或者说整个计算机数据都是由二进制组成的。)
二进制和是如何转换为十进制的?
计算机中有一种存储单位叫做位字节(byte),一个字节有 8 位。
最高位是符号位,其余位数分别表示 1,2,4,8,16,32,64。
如图
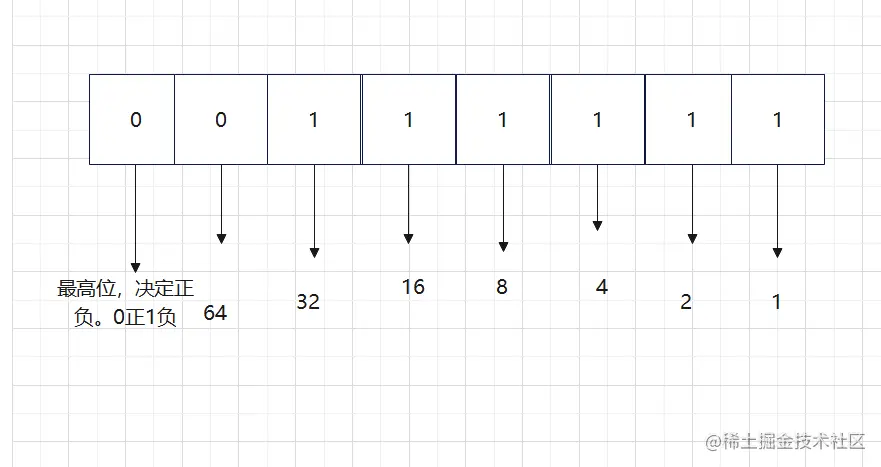
那么图中的 0 和 1 是什么意思呢?1 表示该位置代表的数参与加法运算,0 表示该位置代表的数不参与加法运算。
比如,上图中的 00111111。大家有发现,这串数字前面两为 0 后面都为一。 首先我们看第一个数字 0。上文说过。首位表示符号位。0 表示正数,1 表示负数。。
所以 00111111 表示是一个正的 0111111。
再看 0111111。记得上面的那张图吗,每一位对应的不同的数字。0 表示参与运算,1 表示不参与运算。
所以 0111111 = 32+16+8+4+2+1 === 63;
00111111(二进制) === 63(十进制);
同样的方法。再来几个例子
- 10111111(二进制) === -63(十进制)
- 00000011(二进制) === 1+2 = 3(十进制)
- 10011001(二进制) === 16+8+1 = -25(十进制)(首位为 1 所以是负数)
什么是原码?
原码就是计算机中对数字的二进制定点表示方法,首位为符号位,其余位数表示数字大小。
记得上面二进制和十进制的转换吗。
127(十进制) === 01111111(二进制); 01111111 就是 127 的原码;
3(十进制)=== 00000011(二进制); 00000011 就是 3 的原码;
-25(十进制) === 10011001(二进制); 10011001 就是-25 的原码;
原码的作用,就是以二进制的形式表达一个十进制的数字。
什么是反码?
对于正数来说,原码 === 反码。 比如说:127 十进制) 原码:01111111 反码:(01111111)
对于负数来说:反码 === 原码除符号位不变外,其余位数取反。 比如说:-25(十进制) 原码:10011001 反码:(11100110)
什么是补码?
对于正数来说;补码 === 原码 === 反码 比如说:127(十进制) 原码:01111111 反码:(01111111) 补码:(01111111)
对于负数来说:补码 === 反码 + 1; 比如说:-25(十进制) 原码:10011001 反码:(11100110) 补码:(11100111)
二进制数要如何运算?
因为二进制只存在 0 和 1,所以,当二进制进行运算的时候,大于 1 的数需要进 1 变 0.这就像我们十进制中的大于 10 的数需要进 1 变 0 一样。
举个例 00000001 + 00000001 === 00000010。 某尾两个 1 相加大于 1,所以向前进一。该位归 0
画了个草图,大伙凑合着看看。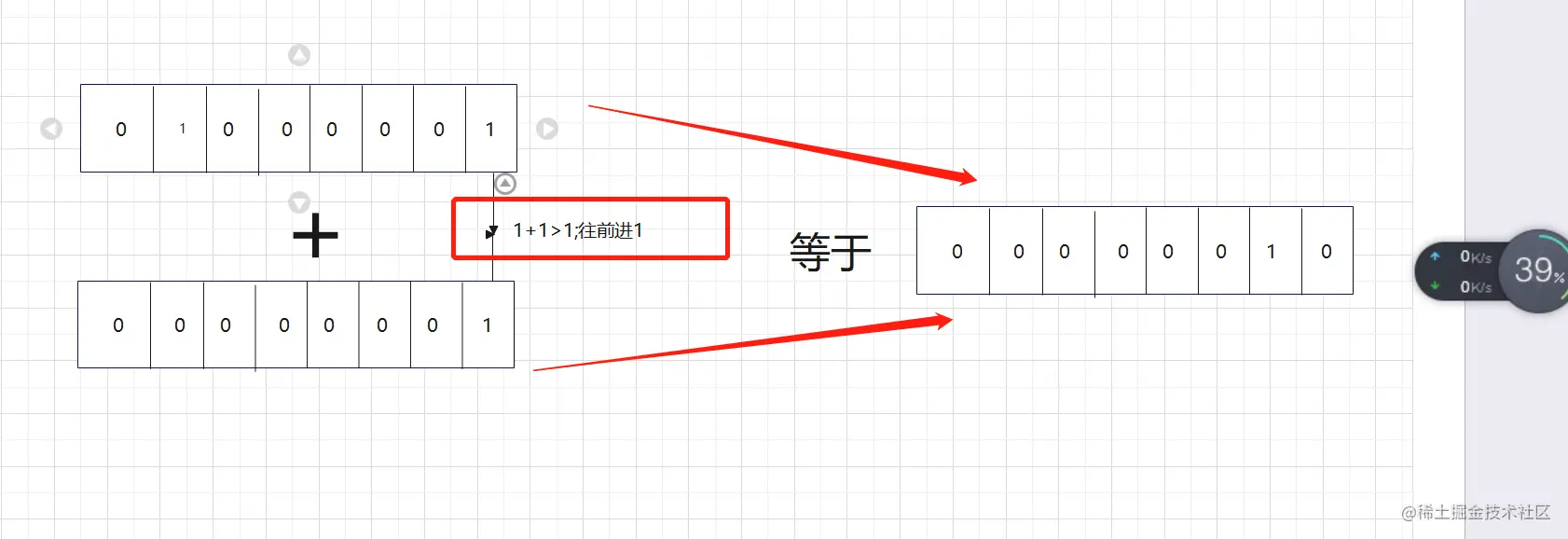
知道了这个机制后我们来尝试下把十进制数转化为二进制计算。
7+25 === 32;
7(十进制) === 00000111(二进制的 7);
25(十进制) === 00011001 (二进制的 25);
00011001 (二进制的 25) + 00000111(二进制的 7) === 00100000(二进制);
我们将 00100000(二进制)再重新为十进制:00100000 === 32 === 7+25 === 00011001 (二进制的 25) + 00000111(二进制的 7);
这个计算好像没问题。但如果参与运算的数字中有一个负数,那就麻烦了。
举个例子 -7+25 === 18;
-7(十进制) === 10000111(二进制的-7);
25(十进制) === 00011001 (二进制的 25);
00011001 (二进制的 25) + 10000111(二进制的-7) === 10100000(二进制);
我们再把 10100000 转回十进制:10100000 ==== -32;

-7+25 的二进制算法转换回来居然是-32;这明显不对啊。
所以。这里就拓展出了另一个概念,二进制中,参与运算的不是原码;而是补码。 或许已经有小伙伴发现了。上面我们出错的运算是我们在使用原码运算并且包含负数的前提条件下。
而正是因为存在这个问题,才会有反码和补码的概念。在计算机中,参与运算的并非原码而是补码。
还是拿-7+25 举个例子;
-7+25 === 18;
-7(十进制) 原码:10000111 补码:11111001 ;
25(十进制) 原码:00011001 补码:00011001;
00011001 (25 的补码) + 11111000(-7 的补码) === 00010010 ;
我们再把 00010010 转回十进制:10100000 ==== 18;
像这样使用补码去运算,可以在即使是负数的情况下也保证运算正确。
一个有意思的现象
原码的范围是 -127 - 127
反码的范围是 -127 - 127
但是补码的范围确是 -128 - 127
总结
- 计算机中无法存储十进制数据,只能存储二进制数据。
- 二进制有三种码型:原码,反码,补码。
- 参与运算的都是补码。
- 正数的反码 === 该数的补码 === 该数的原码
- 负数的反码 === 该数符号位不变,其余位数取反
- 负数的补码 === 该数的反码+ 1
- 10000000 === -128 !== -0
- 00000000 === 0
- 补码的范围可以表示的区间为-128 -127,但原码和反码均为-127 - 127
作者:工边页字 链接:https://juejin.cn/post/7151364978300174344 来源:稀土掘金 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。